có ai online ko nhề?

5+949+555+666+999+888+777=?

555+888+654+978+12321+=?

546+456+565+5+94+6+5++5+6+5++55+56+5+54+4+5+5+5++9+9+96+56+5+5+6+6+65+6+6+6+6+6+5+56++5+5+5+5+5+6+66+6+6+6+6+6+6+6+6+6+6+6+6+6+6+6+6+6+6+5+56+59+9+99+9+9+9+9+6+3+3+3+3+3+3+3+2+2+2+2++1+1+1+1+1+1+897=?

28+5465+9595+459+495+5++65+5+6+459+6+5+594+8595+4+895+945+945+58+4795+85+89+96+95+62+2+626+526+52+65+5+85=?

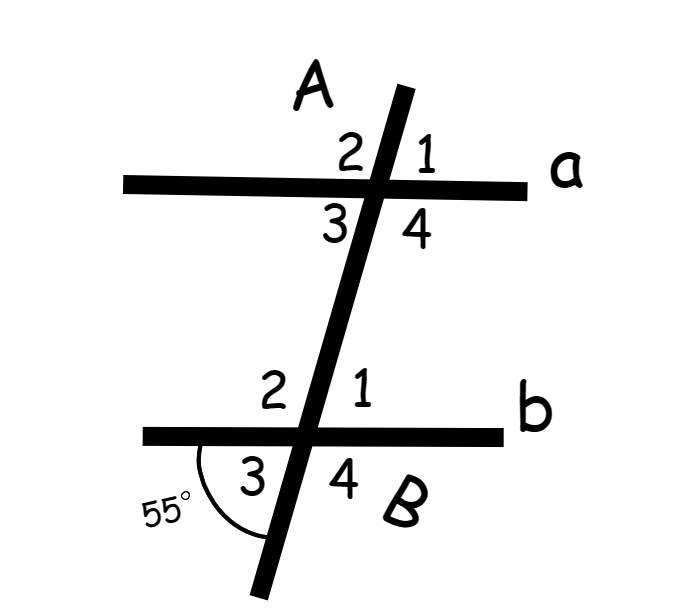
a) \(\widehat{B_1}=\widehat{B_3}=55^o\)

Hai góc đối đỉnh

Mà: \(\widehat{B_3}+\widehat{B_4}=180^o\) (kề bù)

\(\Rightarrow\widehat{B_4}=180^o-55^o=125^o\)

Mà: \(\widehat{B_2}=\widehat{B_4}=125^o\) (đối đỉnh)

b) Ta có: a//b

\(\Rightarrow\widehat{B_3}=\widehat{A_3}=55^o\)

Hai góc đồng vị

Mà: \(\widehat{B_2}=\widehat{A_4}=125^o\)

Hai góc so le trong

Mà: \(\widehat{B_1}=\widehat{A_1}=55^o\)

Đồng vị

Mà: \(\widehat{B_2}=\widehat{A_2}=125^o\)

Hai góc đồng vị

Hình đâu bạn?

Bổ sung giả thiết là \(n\) điểm đó nằm trên \(xy\)

Số các tia có gốc O là \(n\).

Ta nhận thấy số các tia có gốc là các điểm \(A_i\left(1\le i\le n\right)\) chính là \(A^2_n=\dfrac{n!}{\left(n-2\right)!}=n\left(n-1\right)=n^2-n\)

Từ đề bài, ta suy ra \(n^2-n+n=40\Leftrightarrow n^2=40\), vô lí.

(Mình nghĩ đề bài là 49 tia thì khi đó \(n=7\))

giúp em với

em ko biết cô hỏi xà lơ rách việc tự đi mà giải