cho hình bình hành ABCD , O là giao điểm 2 đg chéo 1 đg thẳng đi qua O cắt các cạnh AB và CD theo thư tự ở M và N
CM: M đối xứng với M qua O
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh AB và CD theo thứ tự ở M và N. Chứng minh rằng điểm M đối xứng với điểm N qua O.
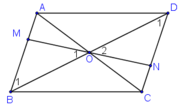
+ ABCD là hình bình hành có O là giao điểm hai đường chéo
⇒ OB = OD.
+ ABCD là hình bình hành ⇒ AB // CD ⇒ 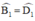 (Hai góc SLT).
(Hai góc SLT).
Hai tam giác BOM và DON có:
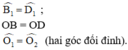
⇒ ΔBOM = ΔDON (g.c.g)
⇒ OM = ON
⇒ O là trung điểm của MN
⇒ M đối xứng với N qua O.
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh AB và CD theo thứ tự ở M và N. Chứng minh rằng điểm M đối xứng với điểm N qua O.
Hướng dẫn:Ta có:ABCD là hình bình hành(gt) =>..............................................
Chứng minh:∆BOM = ∆DON (g.c.g)
Chứng minh: O là trung điểm của MN
=> M đối xứng với N qua O(đpcm)
Xét ΔAOM và ΔCON có
\(\widehat{MAO}=\widehat{NCO}\)
OA=OC
\(\widehat{AOM}=\widehat{CON}\)
Do đó: ΔAOM=ΔCON
Suy ra:OM=ON
hay M và N đối xứng nhau qua O
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh AB và CD theo thứ tự ở M và N. Chứng minh rằng điểm M đối xứng với điểm N qua O ?
Bài giải:
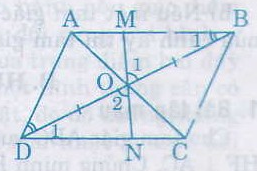
Hai tam giác BOM và DON có
ˆB1B1^ = ˆD1D1^ (so le trong)
BO = DO (tính chất)
ˆO1O1^ = ˆO2O2^ (đối đỉnh)
nên ∆BOM = ∆DON (g.c.g)
Suy ra OM = ON.
O là trung điểm của MN nên M đối xứng với N qua O
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt các cạnh AB và CD theo thứ tự ở M và N. Chứng minh rằng điểm M đối xứng với điểm N qua O.
+ ABCD là hình bình hành có O là giao điểm hai đường chéo
\(\Rightarrow OB=OD\)
+ ABCD là hình bình hành \(\Rightarrow AB//CD\Rightarrow\widehat{B}_1=\widehat{D}_1\) ( hai góc so le trong )
Hai tam giác BOM và DON có:
\(\widehat{B_1}=\widehat{D}_1\)
OB = OD
\(\widehat{O}_1=\widehat{O}_2\) ( hai góc đối đỉnh )
\(\Rightarrow\Delta BOM=\Delta DON\left(g.c.g\right)\)
\(\Rightarrow OM=ON\)
\(\Rightarrow\) O là trung điểm của MN
\(\Rightarrow\) M đối xứng với N qua O.
Vậy M đối xứng với N qua O
Chúc bạn học tốt !!!
+ ABCD là hình bình hành có O là giao điểm hai đường chéo
=> OB = OD.
+ ABCD là hình bình hành => AB // CD => \(\widehat{B_1}=\widehat{D_1}\)( Hai góc SLT ).
Hai tam giác : BOM và DON có :
\(\widehat{B_1}=\widehat{D_1}\)
OB = OD
\(\widehat{O_1}=\widehat{O_2}\)( 2 góc đối đỉnh )
=> ΔBOM = ΔDON (g.c.g)
=> OM = ON
=> O là trung điểm của MN
=> M đối xứng với N qua O.
Hai tam giác BOM và DON có:
Sr , olm lỗi nên phần dưới bị cắt , bổ sung thêm ạ ):
\(\widehat{B_1}=\widehat{D_1}\)
OB = OD
\(\widehat{O_1}=\widehat{O_2}\)( 2 góc đối đỉnh )
=> ΔBOM = ΔDON (g.c.g)
=> OM = ON
=> O là trung điểm của MN
=> M đối xứng với N qua O.
Cho hình bình hành ABCD , O là giao điểm của hai đường chéo . Một đường thẳng đi qua O cắt cạnh AB và CD theo thứ tự ở M và N . Chứng minh rằng điểm M đối xứng với điểm N qua O .
Cho hbh ABCD, O là giao điểm của 2 đg chéo AC và BD. Đg thẳng qua O cắt AD tại P và cắt BC tại Q. CMR: a. OP= OQ. b. Đg thẳng đi qua O cắt AB ở M và cắt CD tạo N. CM: PMQN là hình bình hành
Cho hbh ABCD, O là giao điểm của 2 đg chéo AC và BD. Đg thẳng qua O cắt AD tại P và cắt BC tại Q. CMR:
a. OP= OQ.
b. Đg thẳng đi qua O cắt AB ở M và cắt CD tạo N. CM: PMQN là hình bình hành
Cho hbh ABCD, O là giao điểm của 2 đg chéo AC và BD. Đg thẳng qua O cắt AD tại P và cắt BC tại Q. CMR:
a. OP= OQ.
b. Đg thẳng đi qua O cắt AB ở M và cắt CD tạo N. CM: PMQN là hình bình hành
help!
Cho hình bình hành ABHE, gọi O là giao điểm của 2 đường chéo. Một đường thẳng đi qua Ở cắt các cạnh AB và HE theo thứ tự ở C và D.
chứng minh rằng điểm C đối xứng với điểm D qua O
Xét ΔOAC và ΔOHD có
\(\widehat{OAC}=\widehat{OHD}\)
OA=OH
\(\widehat{AOC}=\widehat{HOD}\)
Do đó: ΔOAC=ΔOHD
Suy ra: OC=OD
hay C đối xứng với D qua O