Bài giải:
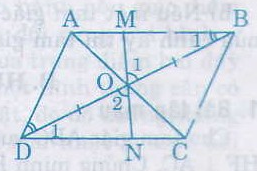
Hai tam giác BOM và DON có
ˆB1B1^ = ˆD1D1^ (so le trong)
BO = DO (tính chất)
ˆO1O1^ = ˆO2O2^ (đối đỉnh)
nên ∆BOM = ∆DON (g.c.g)
Suy ra OM = ON.
O là trung điểm của MN nên M đối xứng với N qua O
Bài giải:

Hai tam giác BOM và DON có
ˆB1B1^ = ˆD1D1^ (so le trong)
BO = DO (tính chất)
ˆO1O1^ = ˆO2O2^ (đối đỉnh)
nên ∆BOM = ∆DON (g.c.g)
Suy ra OM = ON.
O là trung điểm của MN nên M đối xứng với N qua O
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Một đường thẳng đi qua O cắt hai cạnh đối AD, BC ở E và F. Chứng minh rằng các điểm E và F đối xứng với nhau qua điểm O
Cho hình bình hành ABCD, O là giao điểm của hai đường chéo. Qua O, vẽ đường thẳng cắt hai cạnh AB, AC ở E và F. Qua O vẽ đường thẳng cắt hai cạnh AD, BC ở G và H.
Chứng minh rằng EGFH là hình bình hành ?
Cho hình bình hành ABCD lấy M sao cho B là trung điểm của AM , lấy điểm N sao cho D là trung điểm của AN . Chứng minh a) M và N đối xứng với nhau qua C b) Ba đường thẳng AB,BN,DM đồng quy c) Gọi BN cắt CD ở O,AO cắt CN ở I.Chứng minh NI=2/3NC
Bài 4.Cho hình bình hành ABCD , O là giao điểm hai đường chéo. Lấy E thuộc AB, F là giao điểm của EO và CD.
1)Chứng minh tứgiác AECF là hình bình hành
2) Kẻ FH//AC ( H thuộc AD), FG//BD ( G thuộc BC).Chứng minh H đối xứng với G qua Ovà tứgiác EHFG là hình bình hành
Cho hình bình hành ABCD có O là giao điểm hai đường chéo, kẽ AH và CK vuông góc với DB lần lượt tại H và K. Chứng minh:
a/ AHCK là hình bình hành.
b/ H đối xứng với K qua O.
Cho góc xOy và điểm A nằm trong góc đó
a) Vẽ điểm B đối xứng với O qua A. Qua B kẻ đường thẳng song song với Ox, cắt Oy ở C. Gọi D là giao điểm của CA và Ox. Chứng minh rằng các điểm C và D đối xứng với nhau qua điểm A
b) Từ đó suy ra cách dựng đường thẳng đi qua A, cắt Ox, Oy ở D, C sao cho A là trung điểm của CD
Cho tam giác ABC, D là trung điểm của AB, E là trung điểm của AC. Gọi O là một điểm bất kì nằm trong tam giác ABC. Vẽ điểm M đối xứng với O qua D, vé điểm N đối xứng với O qua E.
Chứng minh rằng MNCB là hình bình hành ?
cho tam giác abc vuông góc tại đỉnh A,đường cao AH. gọi D và E theo thứ tự là các điểm đối xứng của điểm H qua các cạnh AB,AC và M là giao điểm của HD với AB,N là giao điểm của HE và AC a.C/M A là trung điểm của đoạn thẳng DE b.C/M MN=AH c.C/M tứ giác BDEC là hình thang vuông
Bài 6. Cho tứgiácABCD. Gọi M, N, P,Q lần lượt là trung điểm các cạnh AB, BC, CD, DA. O là một điểm bất kì trong tứ giác. A’,B’,C’, D’là các điểm đối xứng với O quaM,N,P,Q. Chứng minh tứgiác A’B’C’D’ là hình bình hành