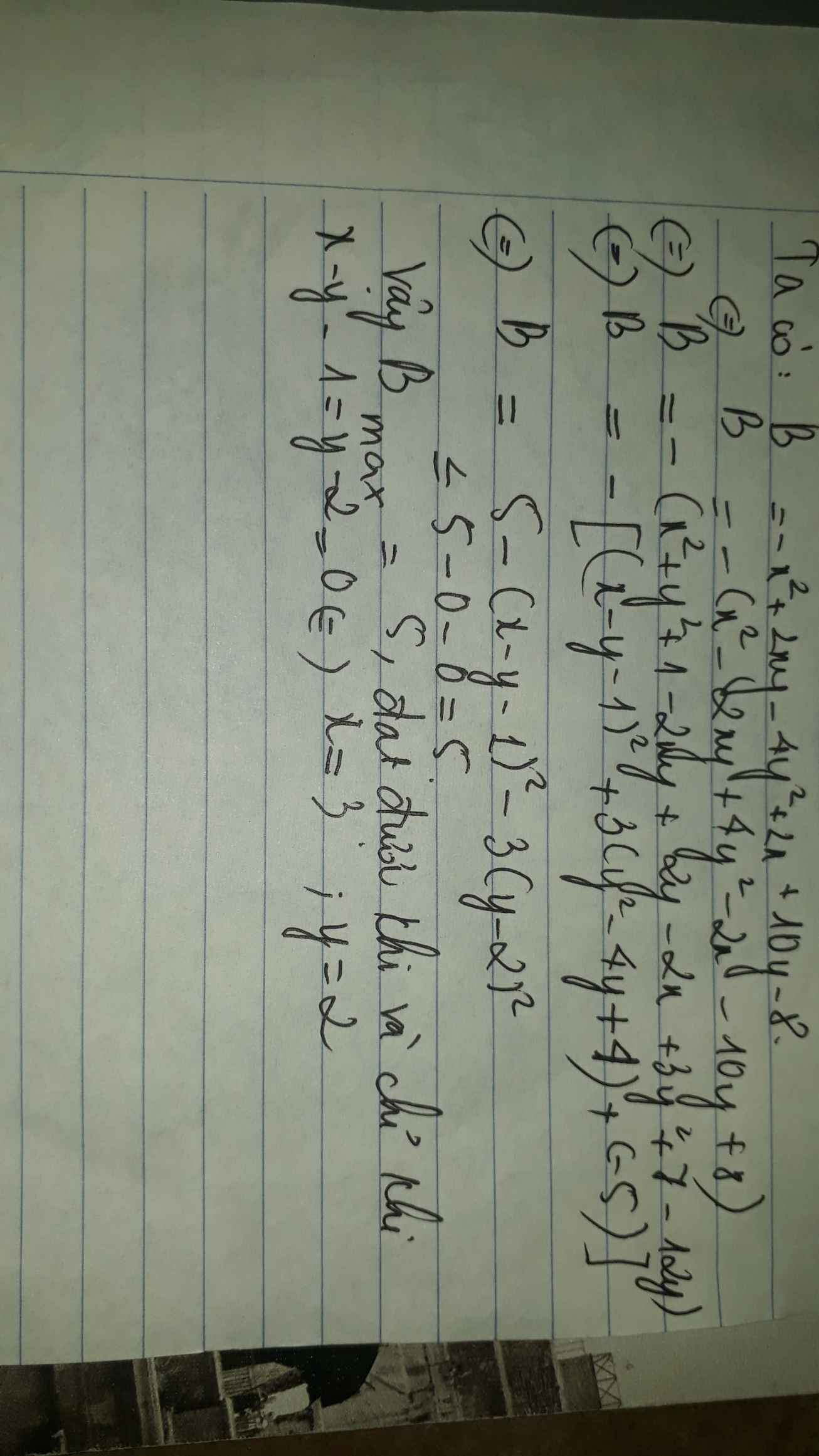\(A=-x^2+2xy-4y^2+2x+10y-8\)

\(=-\left(x^2-2xy+4y^2-2x-10y+8\right)\)

\(=-\left[\left(x-y-1\right)^2+3\left(y-2\right)^2-5\right]\)

\(=5-\left(x-y-1\right)^2-3\left(y-2\right)^2\le5\)

Dấu"=" xảy ra  <=>  \(\hept{\begin{cases}x-y-1=0\\y-2=0\end{cases}}\) <=>  \(\hept{\begin{cases}x=3\\y=2\end{cases}}\)

Vậy MAX  \(A=5\)khi  \(x=3;\)\(y=2\)

\(A=-x^2+2xy-4y^2+2x+10y-8\)

\(=-x^2+2xy-y^2-3y^2+2x-2y+12y-12+4\)

\(=-\left(x^2-2xy+y^2\right)+\left(2x-2y\right)-1-\left(3y^2-12y+12\right)+5\)

\(=-\left(x-y\right)^2+2\left(x-y\right)-1-3\left(y-2\right)^2+5\)

\(=-\left[\left(x-y\right)^2-2\left(x-y\right)+1\right]\)\(-3\left(y-2\right)^2+5\)

\(=-\left(x-y-1\right)^2-3\left(y-2\right)^2+5\)

\(A_{max}=5\Leftrightarrow\hept{\begin{cases}\left(x-y-1\right)^2=0\\3\left(y-2\right)^2=0\end{cases}\Rightarrow\hept{\begin{cases}x-y-1=0\\y-2=0\end{cases}}}\)

\(\Rightarrow\hept{\begin{cases}x-y-1=0\\y=2\end{cases}}\)\(\Rightarrow x-2-1=0\Leftrightarrow x=3\)

\(KL:A_{max}=5\Leftrightarrow x=3;y=2\)

Ta có \(A=-x^2+2xy-4y^2+2x+10y-3\) 

\(A=-x^2+2\left(y+1\right)x-4y^2+10y-3\)

\(A=-x^2+2\left(y+1\right)x-\left(y+1\right)^2-3y^2+12y-2\)

\(A=-\left[x-\left(y+1\right)\right]^2-3\left(y^2-4y+4\right)+10\)

\(A=-\left(x-\left(y+1\right)\right)^2-3\left(y-2\right)^2+10\) \(\le10\)

Dấu "=" xảy ra \(\Leftrightarrow\left\{{}\begin{matrix}x=y+1\\y-2=0\end{matrix}\right.\Leftrightarrow\left(x,y\right)=\left(3,2\right)\)

Vậy \(max_A=10\)

?

\(-x^2+2xy-4y^2+2x+10y-8\)

\(=-\left(x^2-2xy+y^2\right)+2\left(x-y\right)+12y-8-3y^2\)

\(=-\left(x-y\right)^2+2\left(x-y\right)-3\left(y^2-4y+4\right)+4\)

\(=-\left[\left(x-y\right)^2-2\left(x-y\right)+1\right]-3\left(y-2\right)^2+5\)

\(=-\left(x-y-1\right)^2-3\left(y-2\right)^2+5\)

\(=-\left[\left(x-y-1\right)^2+3\left(y-2\right)^2\right]+5\le5\forall x;y\)

Dấu " = " xảy ra

\(\Leftrightarrow\left\{{}\begin{matrix}\left(x-y-1\right)^2=0\\3\left(y-2\right)^2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x-y-1=0\\\left(y-2\right)^2=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x-y=1\\y-2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=y+1\\y=2\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2\end{matrix}\right.\)

Vậy GTLN của biểu thức trên là : \(5\Leftrightarrow\left\{{}\begin{matrix}x=3\\y=2\end{matrix}\right.\)

\(C=-x^2+2xy-4y^2+2x+10y-3\)

\(=-\left(x^2+2xy-y^2\right)+2x-2y-1-3y^2+12y-12+10\)

\(=-\left(x-y\right)^2+2\left(x-y\right)-1-3\left(y^2-4y+4\right)+10\)

\(=-\left(x-y-1\right)^2-3\left(y-2\right)^2+10\le10\forall x;y\)

Dấu "=" xảy ra \(\Leftrightarrow\hept{\begin{cases}x-y-1=0\\y-2=0\end{cases}\Leftrightarrow\hept{\begin{cases}x=3\\y=2\end{cases}}}\)

Vậy \(C_{max}=10\) tại x = 3; y = 2

-A= x^2-2xy+4y^2-2x-10y+8 
-A= ( x^2+y^2+1-2xy-2x+2y) +(3y^2-12y+7) 
-A=(x-y-1)^2+ 3(y^2-4y+7/4)=(x-y-1)^2+3(y-2)^2-27/4>=-... nen A<= 27/4 

(ko biết có đúng hay ko)

-A= x^2-2xy+4y^2-2x-10y+8 
-A= ( x^2+y^2+1-2xy-2x+2y) +(3y^2-12y+7) 
-A=(x-y-1)^2+ 3(y^2-4y+7/4)=(x-y-1)^2+3(y-2)^2-27/4>=-... nen A<= 27/4 

tích đúng mình giải cho