Cho 3 đường thẳng xx'; yy'; zz' cắt nhau tại O
CMR: tồn tại ít nhất 1 góc có đỉnh O không \(\le60^o\)
Cho 2 đường thẳng xx' và yy'.Một đường thẳng thứ 3 cắt xx' ở A,cắt yy' ở B biết rằng 2 tia Ax và By cùng ở trên một nửa mặt phẳng có bờ là đường thẳng AB,XAB + BAx' + ABy = 315 độ và BAx'= 3 lần BAx.Chứng minh xx' song song với yy'
Cho 2 đường thẳng xx', yy'cắt nhau tại O. Trên xx' lấy 3 điểm E, M, N sao cho OE = OM = MN. Chứng minh rằng 3 đường thẳng AE, BN, CM đồng quy.
Cho hai đường thẳng xx'/yy'. Lấy điểm A và B lần lượt thuộc đường thẳng xx' và yy'. Trong nửa mặt phẳng bờ xx' chứa đường thẳng yy' kẻ tia Az và trong nửa mặt phẳng bờ yy' chứa đường thẳng xx' kẻ tia Bt sao cho zAx=tBy'. Lấy hai điểm C thuộc Az và D thuộc Bt.
a) Chứng minh rằng ACD=CDB
b) Kẻ các tia phân giác Am của zAx và tia phân giác Bn của tBy'. Chứng minh rằng Am//Bn
Mk đg cần gấp. TKS mn
Cho 2 đường thẳng xx' và yy'. Một đường thẳng thứ 3 cắt xx' và yy' lần lượt tại A và B. Biết 2 tia Ax và By cùng ở trên 1 nửa mặt phẳng có bờ là đường thẳng AB sao cho xAB+BAx'+ABy=315 độ và BAx' = 3 BAx
a) Viết giả thiết, kết luận
b) Chứng minh xx' song song yy'
Cho đường thẳng xx' , trên đường thẳng xx' lấy điểm O, qua O vẽ đường thẳng yy'. Hãy chứng tỏ góc yOx bằng góc x'Oy'
Gọi O là giao điểm của hai đường thẳng xx' , yy' . Trên tia xx' vẽ đoạn thẳng CD dài 3 cm , trên tia yy' vẽ đoạn thẳng EF sao cho O là trung điểm của mỗi đường thẳng ấy .
Cho hai đường thẳng xx', yy' cắt nhau tại O.
Chứng minh rằng: Nếu M thuộc đường thẳng Ot hoặc thuộc đường thẳng Ot' thì M cách đều hai đường thẳng xx' và yy'.
– TH1: M ∈ Ot
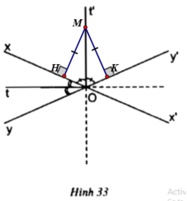
M ∈ Ot do Ot là phân giác của 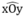 nên M cách đều hai tia Ox và Oy
nên M cách đều hai tia Ox và Oy
⇒ M cách đều xx’, yy’.
Tương tự cho M thuộc tia đối của tia Ot.
- TH2: M ∈ Ot’
M ∈ Ot’ do Ot’ là phân giác của 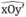 nên M cách đều hai tia Ox, Oy’
nên M cách đều hai tia Ox, Oy’
⇒ M cách đều xx’, yy’.
Tương tự cho M thuộc tia đối của tia Ot’.
Vậy với mọi M thuộc đường thẳng Ot hoặc đường thẳng Ot’, M cách đều xx’ và yy’.
Cho hai đường thẳng xx', yy' cắt nhau tại O.
Chứng minh rằng: Nếu điểm M cách đều hai đường thẳng xx', yy' thì M thuộc đường thẳng Ot hoặc thuộc đường thẳng Ot'.
Ta có M luôn thuộc miền trong của một trong bốn góc:
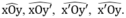
Mà M cách đều xx’ và yy’ nên theo định lý 2 ta có:
+ Nếu M thuộc miền trong góc xOy ⇒ M thuộc tia Ot.
+ Nếu M thuộc miền trong góc xOy’ ⇒ M thuộc tia Ot’.
+ Nếu M thuộc miền trong góc y’Ox’ ⇒ M thuộc tia đối của tia Ot.
+ Nếu M thuộc miền trong góc x’Oy ⇒ M thuộc tia đối của tia Ot’ .
Cho hai đường thẳng xx', yy' cắt nhau tại O.
Chứng minh rằng: Nếu điểm M cách đều hai đường thẳng xx', yy' thì M thuộc đường thẳng Ot hoặc thuộc đường thẳng Ot'.
Ta có M luôn thuộc miền trong của một trong bốn góc:
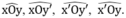
Mà M cách đều xx’ và yy’ nên theo định lý 2 ta có:
+ Nếu M thuộc miền trong góc xOy ⇒ M thuộc tia Ot.
+ Nếu M thuộc miền trong góc xOy’ ⇒ M thuộc tia Ot’.
+ Nếu M thuộc miền trong góc y’Ox’ ⇒ M thuộc tia đối của tia Ot.
+ Nếu M thuộc miền trong góc x’Oy ⇒ M thuộc tia đối của tia Ot’ .
Cho 2 đường thẳng xx' và yy' cắt nhau tại O. Trên xx' lấy điểm A, B, C sao cho OA = AB = BC, trên yy' lấy điểm D, E, F sao cho OD = OE = EF. Chứng minh 3 đường thẳng AD, BF, CE đồng quy.