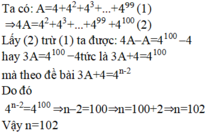A=4+4^2+4^3+...+4^100. Tìm số tự nhiên n biết rằng 3.A+4=4n

Những câu hỏi liên quan
Cho
A
4
+
4
2
+
4
3
+
.
.
.
+
4
99
. Tìm số tự nhiên n biết rằng 3A+4
4
n
-
2
A. n99 B. n100 C. n101 D. n102
Đọc tiếp
Cho A = 4 + 4 2 + 4 3 + . . . + 4 99 . Tìm số tự nhiên n biết rằng 3A+4= 4 n - 2
A. n=99
B. n=100
C. n=101
D. n=102
cho B = 1 + 4 + 42 + 43 + ..........+ 4100
a, tìm số tự nhiên n biết 3B+1=4n
b, tìm chữ số tận cung của B
Cho A=3+3^2+3^3+3^4+...+3^100
Tìm số tự nhiên n sao cho 2A+3=3^4n+1
A= 3 + 32 + 33 + ... + 3100
3A = 32 + 33 + 34 + ... + 3101
3A - A = (32 + 33 + 34 + ... + 3101) - (3 + 32 + 33 + ... + 3100)
2A = 3101 - 3
Ta có: 2A + 3 = 34n+1
= 3101 - 3 + 1 = 34n+1
= 3101 = 34n+1
=> 4n + 1 =101
4n = 101 - 1
4n = 100
n = 100 : 4
n = 25
Đúng 1
Bình luận (0)
A = 3 + 32 + 33 + 34 +......+ 3100
3A = 32 + 33 + 34+.........+ 3100+ 3101
3A - A = 3101 - 3
2A = 3101 - 3
2A + 3 = 3101 - 3 + 3 = 3101
2A + 3 = 34n+1 ⇔ 3101 = 34n+1
101 = 4n + 1
4n = 101 - 1
4n = 100
n = 100 : 4
n = 25
Đúng 0
Bình luận (0)
A= 3 + 32 + 33 + ... + 3100
3A = 32 + 33 + 34 + ... + 3101
3A - A = (32 + 33 + 34 + ... + 3101) - (3 + 32 + 33 + ... + 3100)
2A = 3101 - 3
Ta có: 2A + 3 = 34n+1
= 3101 - 3 + 1 = 34n+1
= 3101 = 34n+1
=> 4n + 1 =101
4n = 101 - 1
4n = 100
n = 100 : 4
n = 25
Đúng 0
Bình luận (0)
cho n thuộc số tự nhiên chứng minh rằng 1/a+1^4 + 3/4+3^4 + ........+2n-1/4+(2n-1)^4 = n^2/4n^2 +1
cho A =3+3^2+3^4+3^5+...+3^100
tìm số tự nhiên n biết rằng 2.A+3=3^n
ta có
\(A=3+3^2+..+3^{100}\)
\(\Rightarrow3A=3^2+3^3+..+3^{100}+3^{101}=\left(3+3^2+..+3^{100}\right)+3^{101}-3\)
hay \(3A=A+3^{101}-3\Leftrightarrow2A+3=3^{101}\)
vậy n=101
Cho A = 3 + 32 + 33 + 34 + 34 + ... + 3100. Tìm số tự nhiên n, biết 2A + 3 = 34n+1
3A = 3^2 + 3^3 + 3^4 + ... + 3^101
3A - A = ( 3^2 + 3^3 + 3^4 + .... + 3^101 ) - ( 3 + 3^2 + 3^3 + ... + 3^100 )
2A = 3^101 - 3
Ta có: 2A + 3 = 3^101 = 3^4 . 25 + 1
Vậy, n=25
TL:
n= 25
k cho mk nhé!
~HT~
Xem thêm câu trả lời
Tìm số tự nhiên n biết rằng:a)
2
n
4
b)
3
n
+
1
27
c)
4
+
4
n
20
d)
15
n
225
Đọc tiếp
Tìm số tự nhiên n biết rằng:
a) 2 n = 4
b) 3 n + 1 = 27
c) 4 + 4 n = 20
d) 15 n = 225
Tìm số tự nhiên n biết rằng:a,
2
n
4
b,
3
n
+
1
27
c,
4
+
4
n
20...
Đọc tiếp
Tìm số tự nhiên n biết rằng:
a, 2 n = 4
b, 3 n + 1 = 27
c, 4 + 4 n = 20
d, 15 n = 225
a, 2 n = 4 ⇒ 2 n = 2 2 ⇒ n = 2
b, 3 n + 1 = 27 = 3 3
⇒ n + 1 = 3 ⇒ n = 2
c, 4 + 4 n = 20
⇒ 4 n = 16 = 4 2 ⇒ n = 2
d, 15 n = 225 = 15 2 ⇒ n = 2
Đúng 0
Bình luận (0)
Cho A= 3+3^2+3^3+3^4+...+3^100
Tìm số tự nhiên N, biết rằng 2A+3=3^N
=>3A=32+32+…+3101
=>3A-A=32+33+…+3101-3-32-…-3100
=>2A=3101-3
=>2A+3=3101=3N
=>N=101
Vậy N=101
Đúng 0
Bình luận (0)
3A = \(3^2+3^3+3^4+...+3^{100}+3^{101}\)
\(\Rightarrow3A-A=\left(3^2+3^3+3^4+...+3^{100}+3^{101}\right)\)- \(\left(3+3^2+3^3+..+3^{100}\right)\)
\(\Rightarrow2A=3^{101}-3\Rightarrow2A+3=3^{101}\)
Vậy n = 101
Đúng 0
Bình luận (0)
3A=32+33+34+35+......+3101
3A-A=(32+33+34+35+.....+3101) - (3+32+33+34+.....+3100)
2A=3101-3
2A+3=3101-3+3
2A+3=3101
Mà theo đề bài thì 2A+3=3n suy ra n=101
Đúng 0
Bình luận (0)
Xem thêm câu trả lời