Tính a + b + c + d + e + f biết a,b,c,d,e,f là các số tự nhiên và abe + bce + cde + dae + abf + bcf + cdf + daf = 29.

Những câu hỏi liên quan
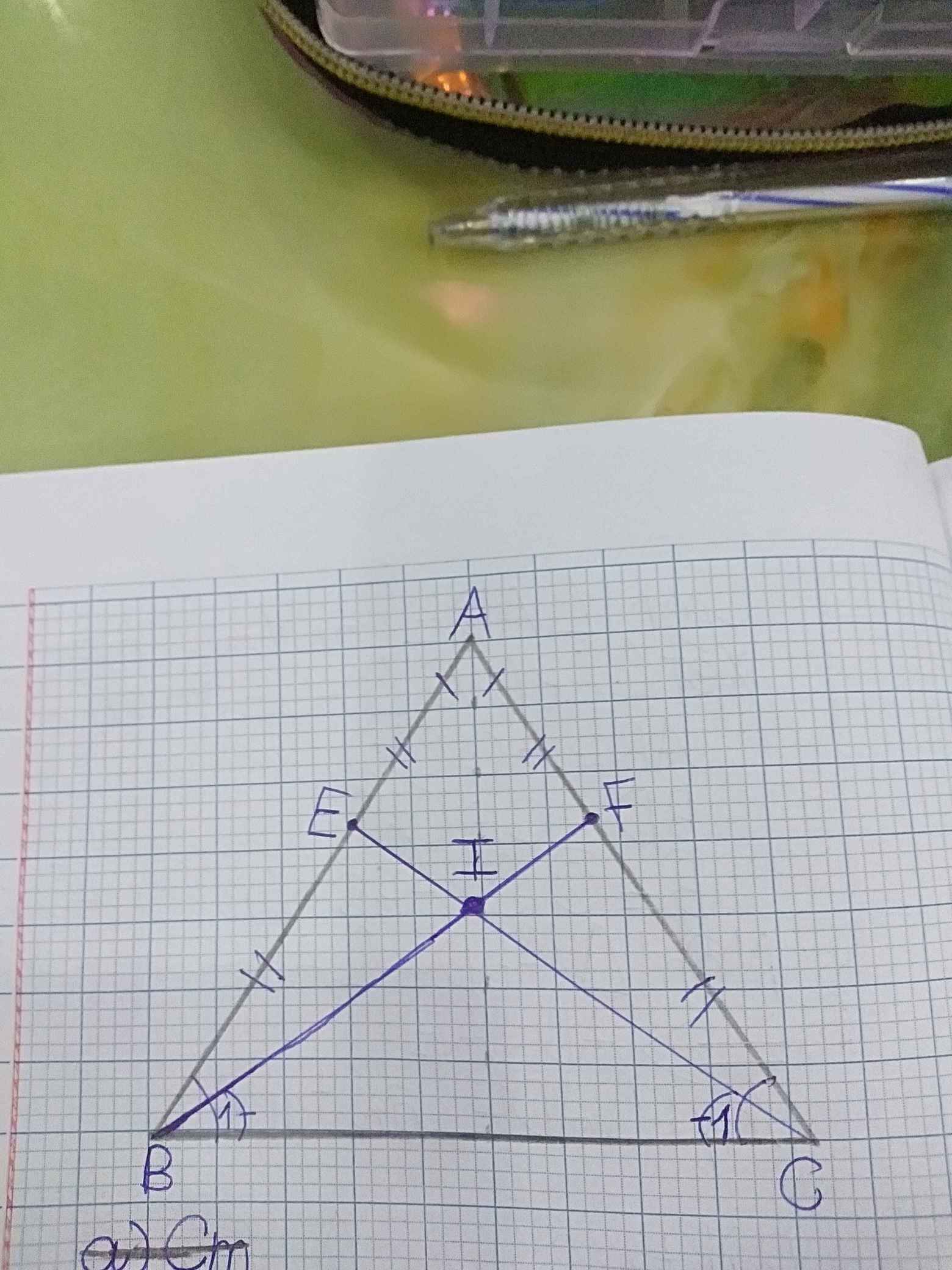
Cho ∆ ABC cân tại A (AB=AC). Gọi E , F lần lượt là trung điểm của AB và AC. a) Chứng minh ∆ ABF=∆ ACE b) Chứng minh ∆ BCE=∆ BCF c) Gọi I là giao điểm của BF và CE. Chứng minh ∆ IBC cân.
Giúp mình bài này nhé mình có gửi hình tam giác như hình vẽ của bài mình ghi ở trên đó mong bạn giúp mình
Đúng 0
Bình luận (0)
a Xét ΔABF và ΔACE có
AB=AC
\(\widehat{FAB}\) chung
AF=AE
Do đó: ΔABF=ΔACE
b: Ta có: ΔABF=ΔACE
nên BF=CE
Xét ΔBEC và ΔCFB có
BE=CF
EC=FB
BC chung
Do đó:ΔBEC=ΔCFB
c: ta có: ΔBEC=ΔCFB
nên \(\widehat{BCE}=\widehat{FBC}\)
hay ΔIBC cân tại I
Đúng 0
Bình luận (0)
Cho các số thực dương a,b,c,d,e,f thoả mãn \(a+b+c+d+e+f=6\)và \(abc+def\ge2.\)Chứng minh rằng: \(ace+afe+cde+abf+bcd+bdf\le6.\)
Tìm các số tự nhiên a, b, c, d, e biết:
101(abcde + abc + abe + ade + cde + c + e + a) = 1001(bcde + bc + be + de + 1)
Nhờ các bạn giải hộ
Tìm số tự nhiên M nhỏ nhất có 4 chữ số thỏa mãn : M= a+b=c+d=e+f
Biết rằng a,b,c,d,e,f là các số tự nhiên khác 0 thỏa mãn a/b = 14/22 , c/d = 11/13 , e/f = 13/17
Ta có:
\(\frac{a}{b}=\frac{14}{22}=\frac{14k}{22k}=>a=14k,b=22k=>M=a+b=14k+22k=36k\)
\(\frac{c}{d}=\frac{11}{13}=\frac{11m}{13m}=>c=11m,d=13m=>M=c+d=11m+13m=24m\)
\(\frac{e}{f}=\frac{13}{17}=\frac{13n}{17n}=>e=13n,f=17n=>M=e+f=13n+17n=30n\)
=>M=36k=24m=30n
=>M chia hết cho 36,24,30
Ta thấy: ƯCLN(36,24,30)=360
=>M chia hết cho 360
=>M=360h
mà M là số bé nhất có 4 chữ số=>h bé nhất
=>999<360h
=>2<h
mà h bé nhất
=>h=3
=>M=3.360=1080
Vậy M=1080
Đúng 0
Bình luận (0)
$\frac{a}{b}=\frac{14}{22}=\frac{14k}{22k}=>a=14k,b=22k=>M=a+b=14k+22k=36k$
Đúng 0
Bình luận (0)
Cho các số thực dương a,b,c,d,e,f thoả mãn a+b+c+d+e+ƒ =6và abc+deƒ ≥2.Chứng minh rằng: ace+afe+cde+abf+bcd+bdf\(\le\)6.
Giúp mình với!
Tìm số tự nhiên M nhỏ nhất có 4 chữ số thỏa man điều kiện M = a+b=c+d=e+f
Biết a,b,c,d,e,f thuộc tập hợp N* và a/b=14/22 ; c/d=11/13; e/f=13/17
\(\frac{a}{b}=\frac{14}{22}=\frac{7}{11}\Rightarrow\frac{a}{7}=\frac{b}{11}=\frac{a+b}{7+11}=\frac{M}{18}\)
\(\frac{c}{d}=\frac{11}{13}\Rightarrow\frac{c}{11}=\frac{d}{13}=\frac{c+d}{11+13}=\frac{M}{24}\)
\(\frac{e}{f}=\frac{13}{17}\Rightarrow\frac{e}{13}=\frac{f}{17}=\frac{e+f}{13+17}=\frac{M}{30}\)
Mà M là số tự nhiên nhỏ nhất có 4 chữa số => M thuộc ƯC(18;24;30)
ƯC(18;24;30) = { 0;360;720;1080;....}
Vậy M = 1080
Đúng 0
Bình luận (0)
Cho 6 số tự nhiên: a, b, c, d, e, f ; biết
- ( a + b ) : 2 = 333
- ( c + d ) : 2 = 555
- ( e + f ) : 2 = 666
- a = d
- b = e
- c = f
Tìm 6 số tự nhiên đó ?
- là âm hay gạch đầu dòng
=>a+b=666;c+d=1010;e+f=1332
=>a+b+c+d+e+f=2408
2(a+b+c)=2408
=>a+b+c=1204
=>a+b=1204-c
=>1204-c=666
=>c=583
=>d=583
tự làm nhé
Xem thêm câu trả lời
Cho hình thang vuông ABCD tại A và D. Gọi E,F lần lượt là trung điểm của AD,BC.Chứng minh:a) ADFcân tại F b) widehat{BAF}widehat{CDF} A B C D E F
Đọc tiếp
Cho hình thang vuông ABCD tại A và D. Gọi E,F lần lượt là trung điểm của AD,BC.
Chứng minh:
a) ADFcân tại F b) \(\widehat{BAF}=\widehat{CDF}\)
Hình thang ABCD có
E là trung điểm của AD
F là trung điểm của BC
Do đó: EF là đường trung bình của hình thang ABCD
Suy ra: EF//AB//CD
mà AB\(\perp\)AD
nên EF\(\perp\)AD
Xét ΔFAD có
FE là đường cao ứng với cạnh AD
FE là đường trung tuyến ứng với cạnh AD
Do đó: ΔFAD cân tại F
b) Ta có: \(\widehat{BAF}+\widehat{DAF}=90^0\)
\(\widehat{CDF}+\widehat{FDA}=90^0\)
mà \(\widehat{FAD}=\widehat{FDA}\)(ΔFAD cân tại F)
nên \(\widehat{BAF}=\widehat{CDF}\)
Đúng 2
Bình luận (0)
Tìm số tự nhiên M nhỏ nhất có 4 chữ số thỏa man điều kiện :
M = a + b = c + d = e + f
Biết a,b,c,d,e,f thuộc N* và \(\frac{a}{b}=\frac{14}{22};\frac{c}{d}=\frac{11}{13};\frac{e}{f}=\frac{13}{17}\)
Giải:
Ta có:
\(\left\{{}\begin{matrix}\dfrac{a}{b}=\dfrac{14}{22}\\\dfrac{c}{d}=\dfrac{11}{13}\\\dfrac{e}{f}=\dfrac{13}{17}\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{b}=\dfrac{7}{11}\\\dfrac{c}{d}=\dfrac{11}{13}\\\dfrac{e}{f}=\dfrac{13}{17}\end{matrix}\right.\)\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{7}=\dfrac{b}{11}\\\dfrac{c}{11}=\dfrac{d}{13}\\\dfrac{e}{13}=\dfrac{f}{17}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}\dfrac{a}{7}=\dfrac{b}{11}=\dfrac{a+b}{7+11}=\dfrac{M}{18}\left(1\right)\\\dfrac{c}{11}=\dfrac{d}{13}=\dfrac{c+d}{11+13}=\dfrac{M}{24}\left(2\right)\\\dfrac{e}{13}=\dfrac{f}{17}=\dfrac{e+f}{13+17}=\dfrac{M}{30}\left(3\right)\end{matrix}\right.\)
Kết hợp \(\left(1\right);\left(2\right)\) và \(\left(3\right)\)
\(\Rightarrow M\in BC\left(18;24;30\right)\)
Mặt khác \(M\) là số tự nhiên nhỏ nhất có 4 chữ số
Nên \(M=1080\)
Vậy \(M=1080\)
Đúng 0
Bình luận (0)