a) C/m H, K ở ngoài đường tròn (O;R).
b)C/m CH=DK.
c)C/m SAHKB=AB*II'.
d)C/m SAHKB=SACB+SADB.
Giải giùm mình câu c và d thôi a và b mình giải rùi. Mình cảm ơn trước nha!!!!!
Những câu hỏi liên quan
Từ điểm A nằm ngoài đường tròn (O), vẽ cát tuyến ABC với đường tròn. Các tiếp tuyến của đường tròn tại B và C cắt nhau ở K. Qua K kẻ đường thẳng vuông góc với AO, cắt AO tại H và đường tròn (O) tại E và F (E nằm giữa K và F). Gọi M là giao điểm của OK và BC.gọi D là giao điểm của BC và EF chứng minh DB.AC =DC.AB
Cho đường tròn 0 và một điểm P ở ngoài đường tròn. Kẻ 2 tiếp tuyến PA, PB với đường tròn O( A,B là tiếp điểm) PO cắt đường tròn tại K và I ( K nằm giữa P và (O) và cắt AB tại H. Gọi D là điểm đối xứng của B qua O, C là giao điểm của PD và đường tròn (O).a, C/m tứ giác BHCP nội tiếpb, C/m AC vuông góc CHc, Đường tròn ngoại tiếp tam giác ACH cắt IC tại M. Tia AM cắt IB tại Q. C/m M là trung điểm AQd, giả sử góc BDC 45 độ tính diện tích tam giác PBD phần nằm ngoài đường tròn O theo R
Đọc tiếp
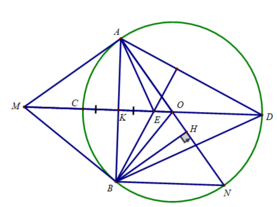
Cho đường tròn 0 và một điểm P ở ngoài đường tròn. Kẻ 2 tiếp tuyến PA, PB với đường tròn O( A,B là tiếp điểm) PO cắt đường tròn tại K và I ( K nằm giữa P và (O) và cắt AB tại H. Gọi D là điểm đối xứng của B qua O, C là giao điểm của PD và đường tròn (O).
a, C/m tứ giác BHCP nội tiếp
b, C/m AC vuông góc CH
c, Đường tròn ngoại tiếp tam giác ACH cắt IC tại M. Tia AM cắt IB tại Q. C/m M là trung điểm AQ
d, giả sử góc BDC = 45 độ tính diện tích tam giác PBD phần nằm ngoài đường tròn O theo R
Qua A ở ngoài đường tròn ( O ; R ) vẽ cát tuyến ABC với đường tròn . Các tiếp tuyến của đường tròn tại B và C cắt nhau ở K . Qua K kẻ đường thẳng vuông với AO cắt AO tại H và cắt đường tròn ( O ) tại E và F ( E nằm giữa K và F ). Gọi M là giao điểm của Ok và BC . Chứng minh :
a) Tứ giác EMOF nội tiếp .
b) AE và AF là các tiếp tuyến của đường tròn ( O ).
Cho đường tròn (O;R) và điểm M ở ngoài đường tròn sao cho OM=8/5 R . Kẻ các tiếp tuyến MA, MB với đường tròn (O) (A, B là các tiếp điểm), đường thẳng AB cắt OM tại K.
c) Kẻ đường kính AN của đường tròn (O). Kẻ BH vuông góc với AN tại H. Chứng minh MB.BN = BH.MO .
c) Ta có: ∠(ABN ) = 90 0 (B thuộc đường tròn đường kính AN)
⇒ BN // MO ( cùng vuông góc với AB)
Do đó:
∠(AOM) = ∠(ANB) (đồng vị))
∠(AOM) = ∠(BOM) (OM là phân giác ∠(AOB))
⇒ ∠(ANB) = ∠(BOM)
Xét ΔBHN và ΔMBO có:
∠(BHN) = ∠(MBO ) = 90 0
∠(ANB) = ∠(BOM)
⇒ ΔBHN ∼ ΔMBO (g.g)
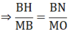
Hay MB. BN = BH. MO
Đúng 1
Bình luận (0)
1 tháng 9 2019 lúc 9:10
Qua A ở ngoài đường tròn ( O ; R ) vẽ cát tuyến ABC với đường tròn . Các tiếp tuyến của đường tròn tại B và C cắt nhau ở K . Qua K kẻ đường thẳng vuông với AO cắt AO tại H và cắt đường tròn ( O ) tại E và F ( E nằm giữa K và F ). Gọi M là giao điểm của OK và BC biết tứ giác EMOF nội tiếp . Chứng minh : AE và AF là các tiếp tuyến của đường tròn ( O ).
Tham khảo :Chứng minh AE, AF là các tiếp tuyến của (O)
Đúng 0
Bình luận (0)
Từ điểm A ở ngoài đường tròn tâm O, vẽ 2 tiếp tuyến AB và AC với (O) (B và C là các tiếp điểm). OA cắt BC tại H, cắt đường tròn (O) tại 2 điểm I và K (I thuộc cung BC nhỏ, K thuộc cung BC lớn). Vẽ đường kính CD, cát tuyến AD cắt (O) tại M. BM cắt OA tại NChứng minh: a) Tứ giác AMHC nội tiếp b) N là trung điểm của AH c) 1/AN1/AI+1/AK
Đọc tiếp
Từ điểm A ở ngoài đường tròn tâm O, vẽ 2 tiếp tuyến AB và AC với (O) (B và C là các tiếp điểm). OA cắt BC tại H, cắt đường tròn (O) tại 2 điểm I và K (I thuộc cung BC nhỏ, K thuộc cung BC lớn). Vẽ đường kính CD, cát tuyến AD cắt (O) tại M. BM cắt OA tại N
Chứng minh: a) Tứ giác AMHC nội tiếp
b) N là trung điểm của AH
c) 1/AN=1/AI+1/AK
a: Xét (O) có
AB,AC là tiếp tuyến
Do đó: AB=AC
=>A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
=>O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA là đường trung trực của BC
=>OA\(\perp\)BC tại H và H là trung điểm của BC
Xét (O) có
ΔDMC nội tiếp
DC là đường kính
Do đó: ΔDMC vuông tại M
=>CM\(\perp\)MD tại M
=>CM\(\perp\)AD tại M
Xét tứ giác AMHC có \(\widehat{AMC}=\widehat{AHC}=90^0\)
nên AMHC là tứ giác nội tiếp
Đúng 1
Bình luận (1)
Cho đường tròn (O; R). Điểm M ở bên ngoài đường tròn sao cho OM= 2R. Kẻ hai tiếp tuyến MA, MB tời đường tròn (A;B là các tiếp điểm). Nối OM cắt AB tại H. Hạ HD vuông góc MA tại D. Điểm C thuộc cung nhỏ AB. Tiếp tuyến tại C của đường tròn (O;R) cắt MA, MB lần lượt tại E và F. Đường tròn đường kính BM cắt BD tại I. Gọi K là trung điểm của OA. Chứng minh ba điểm M, I, K thẳng hàng
Cho đường tròn (o), từ điểm A ở ngoài đường tròn (o) kẻ 2 tiếp tuyến AB, AC( B, C là các tiếp điểm) và cát tuyến ADE đến đường tròn (O)(D, C thuộc (O) và tia AE ko qua O). Gọi K là trung điểm cùa DE.1) C/m 5 điểm A,B,O,K,C cùng thuộc 1 đường tròn.2) Gọi H là giao điểm của OA với BC. Gọi M là giao điểm của Ae và BC. C/m các tứ giác OHMK và DHOE nt.3) C/m AM.AKAD.AE4) Tia OK cắt đường tròn (O) tại T, tia TM cắt đường tròn (O) tại S, tia AS cắt dường tròn (O) tại Q. C/m QM vuông góc với AT.
Đọc tiếp
Cho đường tròn (o), từ điểm A ở ngoài đường tròn (o) kẻ 2 tiếp tuyến AB, AC( B, C là các tiếp điểm) và cát tuyến ADE đến đường tròn (O)(D, C thuộc (O) và tia AE ko qua O). Gọi K là trung điểm cùa DE.
1) C/m 5 điểm A,B,O,K,C cùng thuộc 1 đường tròn.
2) Gọi H là giao điểm của OA với BC. Gọi M là giao điểm của Ae và BC. C/m các tứ giác OHMK và DHOE nt.
3) C/m AM.AK=AD.AE
4) Tia OK cắt đường tròn (O) tại T, tia TM cắt đường tròn (O) tại S, tia AS cắt dường tròn (O) tại Q. C/m QM vuông góc với AT.
Từ điểm A nằm ngoài đường tròn (O), vẽ cát tuyến ABC với đường tròn. Các tiếp tuyến của đường tròn tại B và C cắt nhau ở K. Qua K kẻ đường thẳng vuông góc với AO, cắt AO tại H và đường tròn (O) tại E và F (E nằm giữa K và F). Gọi M là giao điểm của OK và BC. Chứng minh:
a) Tứ giác EMOF nội tiế.
b) AE, AF là tiếp tuyến của đường tròn.
a) Nối CE, CF
Xét \(\Delta CEK\) và \(\Delta CFK\) có:
\(\widehat{ECK}\)= \(\widehat{CFK}\) (vì cùng chắn \(\widebat{CE}\))
\(\widehat{CKF}\) chung
\(\Rightarrow\)\(\Delta EKC~\Delta CKF\left(g.g\right)\)
\(\Rightarrow\frac{EK}{CK}=\frac{CK}{FK}\)
\(\Rightarrow CK^2=EK.FK\)(1)
Vì \(\Delta COK\)vuông tại C, \(CM\perp OK\)
\(\Rightarrow CK^2=MK.OK\)(2)
Từ (1), (2) \(\Rightarrow EK.FK=MK.OK\)
\(\Rightarrow\frac{EK}{MK}=\frac{OK}{FK}\)
Xét \(\Delta MEK\)và \(\Delta KOF\)có:
\(\widehat{MKE}\)chung
\(\frac{EK}{MK}=\frac{OK}{FK}\)
\(\Rightarrow\Delta MEK~\Delta FOK\left(c.g.c\right)\)
\(\Rightarrow\widehat{OFE}=\widehat{EMK}\)
\(\Rightarrow\)Tứ giác EMOF nội tiếp
Vẽ đường tròn (O ; 2cm) . Gọi M là 1 điểm nằm ngoài (O) ở I . Biết OM = 3cm
a, Tính IM
b, Vẽ đường tròn tâm I bán kính IM . Chúng tỏ điểm I nằm ngoài (I;IM)
c, (I;IM) cắt (O ; 2cm) ở P và Q , cắt OM ở K . Chứng tỏ điểm K nằm trong (O;2cm)