cho tam giác ABC có AB=16, AC=14, góc B=600. Tính BC.

Những câu hỏi liên quan
Cho tam giác ABC có AB = 16, AC = 14 và B ^ = 60 0 . Tính BC
A. BC = 10
B. BC = 11
C. BC = 9
D. BC = 12
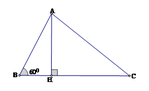
Kẻ đường cao AH
Xét tam giác vuông ABH, ta có:
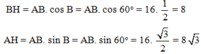
Áp dụng định lý Py-ta-go vào tam giác vuông AHC ta có:
![]()
Suy ra HC = 2.
Vậy BC = CH + HB = 2 + 8 = 10
Đáp án cần chọn là: A
Đúng 0
Bình luận (0)
Cho tam giác ABC có AB = 14 ,AC =16, góc B =60°. Tính BC và diện tích tâm giác ABC
Bài 14: Cho tam giác ABC có BC 16 cm, AB 20 cm, AC 12 cm.a/ Chứng minh tam giác ABC là tam giác vuông. (1,5 điểm) b/ Tính sin A, t B và số đo góc B, góc A. (2 điểm) c/ Vẽ đường cao CH. Tính các độ dài CH , BH, HA. (1,5 điểm) d/ Vẽ đường phân giác CD của ABC. Tính độ dài DB, DA, CD e/ Đường thẳng vuông góc với BC tại B cắt...
Đọc tiếp
Bài 14: Cho tam giác ABC có BC = 16 cm, AB = 20 cm, AC = 12 cm.
a/ Chứng minh tam giác ABC là tam giác vuông. (1,5 điểm)
b/ Tính sin A, t B và số đo góc B, góc A. (2 điểm)
c/ Vẽ đường cao CH. Tính các độ dài CH , BH, HA. (1,5 điểm)
d/ Vẽ đường phân giác CD của ABC. Tính độ dài DB, DA, CD
e/ Đường thẳng vuông góc với BC tại B cắt tia CH tại K. Tính độ dài BK
a: Xét ΔABC có \(AB^2=AC^2+BC^2\)
nên ΔABC vuông tại C
Đúng 1
Bình luận (0)
Tam giác ABC có AB=16; AC=14; góc B=60 độ; góc C > 90 độ. Tính BC
cho tam giác ABC có AB = 14, \(\widehat{C}\) = 120o, BC+AC=16. Tính BC, AC
Cho tam giác ABC vuông tại A có góc B=600 BC=20cm
Tính AB,AC
Kẻ đường cao AH của tam giác. Tính AH,HB,HC
Cho tam giác ABC có 3 góc nhọn, AB=4.5 BC=14 AC=13
a, Tính 3 góc nhọn
b, Tính diện tích tam giác ABC
1) Cho tam giác ABC vuông tại A có góc B = 60độ, AC = 3cm. Tính BC, AB
2) Cho tam giác ABC vuông tại A có BC = 10cm, góc C = 3cm. Tính góc B, AB, AC
3) Cho tam giác ABC vuông tại A có AB = 4cm, góc B = 50 độ. Tính BC, góc C, AC
3:
góc C=90-50=40 độ
Xét ΔABC vuông tại A có sin C=AB/BC
=>4/BC=sin40
=>\(BC\simeq6,22\left(cm\right)\)
\(AC=\sqrt{BC^2-AB^2}\simeq4,76\left(cm\right)\)
1:
góc C=90-60=30 độ
Xét ΔABC vuông tại A có
sin B=AC/BC
=>3/BC=sin60
=>\(BC=\dfrac{3}{sin60}=2\sqrt{3}\left(cm\right)\)
=>\(AB=\dfrac{2\sqrt{3}}{2}=\sqrt{3}\left(cm\right)\)
Đúng 0
Bình luận (1)
Cho tam giác ABC có AB 14, BC 10, AC 16. Trên đường thẳng vuông góc với mặt phẳng (ABC) tại A lấy điểm O sao cho OA 8. Tính khoảng cách từ O đến đường thẳng BC. A. 24 B. 16 C .
8
2
D.
8
3
Đọc tiếp
Cho tam giác ABC có AB = 14, BC = 10, AC = 16. Trên đường thẳng vuông góc với mặt phẳng (ABC) tại A lấy điểm O sao cho OA = 8. Tính khoảng cách từ O đến đường thẳng BC.
A. 24
B. 16
C . 8 2
D. 8 3
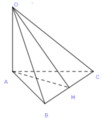
Gọi H là chân đường cao kẻ từ A xuống BC trong tam giác ABC.
+ Ta có: A H ⊥ B C O A ⊥ B C ⇒ B C ⊥ O A H ⇒ O H ⊥ B C ⇒ d(O; BC) = OH
+ Nửa chu vi tam giác ABC: p = 14 + 16 + 10 2 = 20
S A B C = 20 20 − 14 20 − 16 20 − 10 = 40 3 (theo công thức Hê-rông)
Lại có S A B C = 1/2AH.BC ⇒ AH = 2 S A B C B C = 80 3 10 = 8 3 .
+ Tam giác OAH vuông tại A (OA ⊥ AH)
⇒ OH = O A 2 + A H 2 = 8 2 + 8 3 2 = 16.
Vậy d(O; BC) = OH = 16.
Đáp án B
Đúng 0
Bình luận (0)













