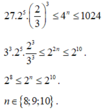\(~~~HD~~~\)

\(1023^{1024}=\left(1023^4\right)^{256}=\left(...1\right)^{256}=\left(.....1\right)\)

4ⁿ = 1024 

4ⁿ = 4⁵

=> n = 5

4ⁿ = 1024 

4ⁿ = 4⁵

=> n = 5

Ta có \(2^x-2^y=1024\Rightarrow x>y\)

Do đó \(2^y\left(2^{x-y}-1\right)=2^{10}\)

Lại có \(2^{x-y}-1\) lẻ và là ước 10 nên \(2^{x-y}-1=1\Rightarrow2^y=2^{10}\)

\(\Rightarrow y=10\Rightarrow2^{x-10}=2^1\Rightarrow x=11\)

Vậy \(\left(x;y\right)=\left(11;10\right)\)

\(1024=2^{10}\)\(\Rightarrow2^y\left(2^m-1\right)=2^{10}.1\Rightarrow\hept{\begin{cases}y=10\\x=11\end{cases}}\)

=> x>y

x-y =m

mk bít lm nè

2^x + 124 = 5^y  (1)

Ta có:

2^x + 124 là số chẵn nếu x lớn hơn hoặc bằng 1,

2^x + 124 là số lẻ nếu x = 0, mặt khác:  5^y là một số lẻ nên suy ra:

=> x = 0

Từ (1) suy ra: 1 + 124 = 5^y

=> 5^y  = 125

5^y  = 5³

=> y = 3.

Kết luận: x = 0 và y = 3.