cho hai đường thẳng xx' và yy' cắt nhau tại O, sao cho góc xOy=36 độ.
a, Tính số đo các góc yOx' ;x'Oy' và y'Ox.
b, Gọi Ot và Ot' lần lượt là tia phân giác của góc xOy và x'Oy'. Chứng minh Ot và Ot' là hai tia đối nhau.
Những câu hỏi liên quan
a/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 900 . Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
b/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 300 . Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
a ) Ta có : xOy + yOx ' = 180 ( kề bù )
\(\Rightarrow\) 90 + yOx ' = 180
\(\Rightarrow\) yOx ' = 180 - 90 = 90
Lại có : xOy + y ' Ox = 180 ( kề bù )
\(\Rightarrow\) 90 + y ' Ox = 180
\(\Rightarrow\) y ' Ox = 180 - 90 = 90
Ta thấy : xOy ' + y ' Ox ' = 180 ( kề bù )
\(\Rightarrow\) 90 + y ' Ox ' = 180
\(\Rightarrow\) y ' Ox ' = 180 - 90 = 90
b ) Ta có : xOy + yOx ' = 180 ( kề bù )
\(\Rightarrow\) 30 + yOx ' = 180
\(\Rightarrow\) yOx ' = 180 - 30 = 150
Lại có : xOy + yOx '= 180 ( kề bù )
\(\Rightarrow\) 30 + yOx ' = 180
\(\Rightarrow\) yOx ' = 180 - 30 = 150
Ta thấy : x ' Oy + y ' Ox ' = 180 ( kề bù )
\(\Rightarrow\) 150 + y ' Ox ' = 180
⇒ y ' Ox ' = 180 - 150 = 3
Bài làm lại :
a ) \(\widehat{xOy}+\widehat{y'Oy}=180^o\)( KB )
\(\widehat{x'Oy}=180^o-\widehat{xOy}=180^o-90^o=90^o\)( Đối đỉnh )
Vậy \(\widehat{xOy}'=\widehat{y'Ox}=90^o\)( Đối đỉnh )
b ) \(\widehat{xOy}+\widehat{x'Oy}=180^o\)( KB )
\(\widehat{x'Oy}=180^o-\widehat{xOy}=180^o-30^o=150^o\)
Vậy \(\widehat{xOy}=\widehat{x'Oy'}=30^o\)( Đối đỉnh )
\(\widehat{yOx'}=\widehat{y'Ox}=150^o\)( Đối đỉnh )
a/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 90 độ . Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
b/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 30 độ . Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
a/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 900.
Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
b/ Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và góc xOy bằng 300.
Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
Bài giải
a) yOx' ; x'Oy' ; y'Ox đều bằng 90 độ
b) yOx' bằng 150 độ ; x'Oy' bằng 30 độ ; y'Ox bằng 150 độ
Học tốt !
Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và
x
O
y
^
90
°
.
Cho biết số đo của các góc
y
O
x
^
,
x
O
y
^
, ...
Đọc tiếp
Hai đường thẳng xx’, yy’ cắt nhau tại điểm O và x O y ^ = 90 ° . Cho biết số đo của các góc y O x ' ^ , x ' O y ' ^ , y ' O x ^ .
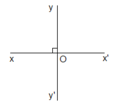
Cho hai đường thẳng xx' và yy' cắt nhau tại O, sao cho xÔy = 36 độ
a) Tính số đo các góc yOx' ; x'Oy' và y'Õ
b) Gọi Ot và Ot' lân lượt là tia phân giác của góc xOy và x'Oy'. Chứng minh Ot và Ot' là hai tia đối nhau
a) ta có O1+O2=180=> O2=180-O1=180-36=144
TA CÓ : O1=O3 =36 ( đối đỉnh )
O2=O4 =144 ( đối đỉnh)
b) ta có góc tOt'= góc tOx+O4+góc y'Ot'= \(\frac{36}{2}\)+144+ \(\frac{36}{2}\)=180
=> Ot và Ot' nằm trên cùng đường thẳng
mặt khác Ot và Ot' cùng chung gốc O
=> Ot và Ot' là 2 tia đối
Đúng 0
Bình luận (0)
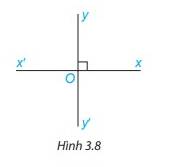
Hai đường thẳng xx’ và yy’ cắt nhau tại O sao cho góc xOy vuông (H.3.8). Khi đó các góc yOx’, x’Oy’, xOy’ cũng đều là góc vuông. Vì sao?
Góc x’Oy’ và xOy là hai góc đối đỉnh nên \(\widehat {x'Oy'} = \widehat {xOy} = 90^\circ \)
Góc xOy’ và xOy là hai góc kề bù nên
\(\begin{array}{l}\widehat {xOy'} + \widehat {xOy} = 180^\circ \\ \Rightarrow \widehat {xOy'} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {xOy'} = 180^\circ - 90^\circ = 90^\circ \end{array}\)
Góc x’Oy và xOy là hai góc kề bù nên
\(\begin{array}{l}\widehat {x'Oy} + \widehat {xOy} = 180^\circ \\ \Rightarrow \widehat {x'Oy} + 90^\circ = 180^\circ \\ \Rightarrow \widehat {x'Oy} = 180^\circ - 90^\circ = 90^\circ \end{array}\)
Đúng 1
Bình luận (0)
Hai đường thẳng xx’, yy’ cắt nhai tại điểm O và ∠(xOy) ̂=90o. Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox
Hai đường thẳng xx’, yy’ cắt nhai tại điểm O và ∠(xOy) = 30o. Hãy đo và cho biết số đo của các góc yOx’, x’Oy’, y’Ox.
∠(x'Oy') = 30o , ∠(x'Oy) = 150o , ∠(xOy') = 150o.
Đúng 0
Bình luận (0)
cho hai đường thẳng xx và yy cắt nhau tại O. biết x'Oy + xO'y = 120 tính các góc Xoy Yox x'oy y'ox