do AB song song với CD nên ta có \(A+D=180^0\text{ mà }A=D+40^0\Rightarrow D+40^0+D=180^0\Rightarrow\hept{\begin{cases}D=70^0\\A=110^0\end{cases}}\)

\(\Rightarrow C=\frac{A}{2}=55^0\Rightarrow B=180^0-55^0=125^0\)

Vì AB//CD nên \(\left\{{}\begin{matrix}\widehat{A}+\widehat{D}=180^0\\\widehat{B}+\widehat{C}=180^0\end{matrix}\right.\left(trong.cùng.phía\right)\)

Mà \(\widehat{A}-\widehat{D}=30^0;\widehat{B}=2\widehat{C}\Rightarrow\left\{{}\begin{matrix}\widehat{A}=\left(180^0+30^0\right):2=105^0\\\widehat{D}=180^0-105^0=75^0\\3\widehat{C}=180^0\end{matrix}\right.\)

\(\Rightarrow\widehat{C}=60^0\Rightarrow\widehat{B}=120^0\)

có góc B=60 độ r tính làm j

góc A+D=180độ(1)

góc A=3*D(2)

từ 2 suy ra 180 độ +gócD thay thế vào 1

góc A+góc D+3D=180 độ

góc 4D=180 độ

góc 4D=180/4=45 ĐỘ

góc B=45*3=135 độ

cm tưng tự

hfthfygh

SABCD = (AB + CD) x AD : 2

          = (50 + 60) x (40 + 10) : 2 = 2750 (cm2 )

SAND = SABCD – (SABN + SNDC)

        = 2750 – (1/(2 ) x 50 x 40) + (1/(2 ) x 60 x 10)

        = 1450 (cm2)

SAND = 1/(2 ) x AD x MN => MN = 2 x SAND : AD

                                            = 2 x 1450 : 50 = 58 (cm2)

SABMN = (50 + 58) x 40 : 2 = 2160 (cm2)

Bài 5

\(\widehat{A}+\widehat{D}=180^o\) (Hai góc trong cùng phía bù nhau)

\(\widehat{DAx}=\widehat{BAx}=\dfrac{\widehat{A}}{2}\) (gt)

\(\widehat{ADy}+\widehat{CDy}=\dfrac{\widehat{D}}{2}\) (gt)

\(\Rightarrow\widehat{DAx}+\widehat{ADy}=\dfrac{\widehat{A}}{2}+\dfrac{\widehat{D}}{2}=\dfrac{180^o}{2}=90^o\)

Xét tg ADE có

\(\widehat{AED}=180^o-\left(\widehat{DAx}+\widehat{ADy}\right)=180^o-90^o=90^o\) (Tổng các góc trong của tg bằng 180 độ)

\(\Rightarrow Ax\perp Dy\)

Bài 6:

a/

Ta có

AB//CD => AB//DE

BE//AB (gt)

=> ABED là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau từng đôi một là hbh)

=> AB = DE; AD = BE (Trong hình bình hành các cạnh đối nhau thì bằng nhau)

b/

CD - DE = CE

Mà AB = DE (cmt)

=> CD - AB = CE

c/

Xét tg BCE có

BC+BE>CE (trong tg tổng độ dài 2 cạnh lớn hơn độ dài cạnh còn lại)

Mà CE = CD - DE và DE = AB (cmt) và BE = AD

=> BC+BE = BC + AD>CE = CD - AB

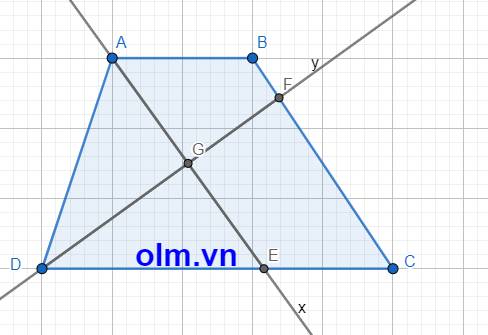
Gọi G là giao điểm của hai đường phân giác Ax và By 

Ta có: \(\widehat{ADG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) ( vì DG là phân giác góc ADE)

           \(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{DAB}\)( vì AG là phân giác góc DAB )

     ⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\)\(\widehat{ADE}\) + \(\dfrac{1}{2}\)\(\widehat{DAB}\) = \(\dfrac{1}{2}\)(\(\widehat{ADE}\) + \(\widehat{DAB}\)) 

           \(\widehat{ADE}\) + \(\widehat{DAB}\) = 180⁰ (vì hai góc là hai góc trong cùng phía)

      ⇒ \(\widehat{ADG}\) + \(\widehat{DAG}\) = \(\dfrac{1}{2}\) \(\times\) 180⁰ = 90⁰

          Xét tam giác ADG có: \(\widehat{GAD}\) + \(\widehat{ADG}\) + \(\widehat{DGA}\) = 180⁰ (tổng ba góc trong 1 tam giác bằng 180⁰)

               ⇒ \(\widehat{DGA}\)  = 180⁰ - 90⁰ = 90⁰

Vậy tam giác ADG vuông tại G ⇒AE \(\perp\) DG (đpcm)