cho góc xOy = 60 độ.Oz là tia phân giác,M là điểm trên tia Oz sao cho khoảng cách từ M đến cạch Oy là 5 cm.khoảng cách từ M đến cạch Ox là ?![]()

Những câu hỏi liên quan
Cho góc xOy =60 độ .Oz là tia phân giác,M là điểm trên tia Oz sao cho khoảng cách từ M đến cạch là 5 cm.Khoảng cách từ Mđến Oy là ?![]()
m đến cạch oy là 5cm khoảng cách từ m đến cách oz là?
Đúng 0
Bình luận (0)
Cho góc xOy = 60 độ,Oz là tia phân giác,M là điểm trên tia Oz sao cho khoảng cách từ M đến cạnh Oy là 5cm.Khoảng cách từ M đến cạnh Ox là bao nhiêu
gọi đường vuông góc với Oy mà MP.
gọi đường vuông góc với Ox là MQ.
xét tam giác OMP và tam giác OMQ, ta có: OM chung.
\(\widehat{MPO}=\widehat{MQO}=90^o\)
\(\widehat{POM}=\widehat{QOM}\)(tia phân giác của Oz).
=> tam giác OMP = QMQ (ch-gn)
=> MP = MQ (cạnh tương ứng)
mà MP = 5 cm
=> MQ = 50 cm
=> khoảng cách từ M -> Ox là 5cm
vì khoảng cách từ M -> Ox là 5 cm nên khoảng cách từ M -> Ox là 5 cm (tính chất của tia phân giác).
Đúng 0
Bình luận (0)
Cho góc x O y ^ có Oz là tia phân giác, M là một điểm trên Oz sao cho khoảng cách từ M đến Oy là 5 cm. Khoảng cách từ M đến Ox là
A. 10 cm
B. 5 cm
C. 30 cm
D. 15 cm
Vì M thuộc Oz là tia phân giác của góc x O y ^ nên M cách đều hai tia Ox và Oy
Vậy khoảng cách từ M đến Ox bằng khoảng cách từ M đến Oy và bằng 5 cm.
Chọn đáp án B
Đúng 0
Bình luận (0)
Cho góc x O y ^ có Oz là tia phân giác, M là một điểm trên Oz sao cho khoảng cách từ M đến Oy là 5 cm. Khoảng cách từ M đến Ox là
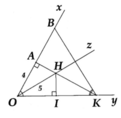
Cho góc xOy, tia phân giác Oz. Trên tia Ox lấy điểm A sao cho OA 4cm. Từ A kẻ đường thẳng vuông góc với Ox cắt Oz tại H, cắt Oy tại K. Lấy điểm B trên tia Ox sao cho A là trung điểm của OB. Hạ
H
I
⊥
O
K
.
a) Chứng minh AH HIb) Biết OH 5 cm, tính khoảng cách từ điểm H đến BK.
Đọc tiếp
Cho góc xOy, tia phân giác Oz. Trên tia Ox lấy điểm A sao cho OA = 4cm. Từ A kẻ đường thẳng vuông góc với Ox cắt Oz tại H, cắt Oy tại K. Lấy điểm B trên tia Ox sao cho A là trung điểm của OB. Hạ H I ⊥ O K .
a) Chứng minh AH = HI
b) Biết OH = 5 cm, tính khoảng cách từ điểm H đến BK.
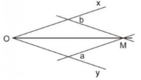
Hình 31 cho biết cách vẽ tia phân giác của góc xOy bằng thước hai lề: Áp một lề của thước vào cạnh Ox, kẻ đường thẳng a theo lề kia. Làm tương tự với cạnh Oy, ta kẻ được đường thẳng b. Gọi M là giao điểm của a và b, ta có OM là tia phân giác của góc xOy. Hãy chứng minh tia OM được vẽ như vậy đúng là tia phân giác của góc xOy. (Gợi ý: Dựa vào bài tập 12 chứng minh các khoảng cách từ M đến Ox và đến Oy bằng nhau (do cùng bằng khoảng cách hai lề của chiếc thước) rồi áp dụng định lí 2) Hình 31
Đọc tiếp
Hình 31 cho biết cách vẽ tia phân giác của góc xOy bằng thước hai lề:
Áp một lề của thước vào cạnh Ox, kẻ đường thẳng a theo lề kia.
Làm tương tự với cạnh Oy, ta kẻ được đường thẳng b.
Gọi M là giao điểm của a và b, ta có OM là tia phân giác của góc xOy.
Hãy chứng minh tia OM được vẽ như vậy đúng là tia phân giác của góc xOy.
(Gợi ý: Dựa vào bài tập 12 chứng minh các khoảng cách từ M đến Ox và đến Oy bằng nhau (do cùng bằng khoảng cách hai lề của chiếc thước) rồi áp dụng định lí 2)
Hình 31
(Từ bài tập 12 ta biết rằng: độ dài đường vuông góc giữa hai đường thẳng song song chính là khoảng cách giữa hai đường thẳng đó.)
Gọi A, B lần lượt là chân đường cao hạ từ M xuống Ox, Oy ⇒ MA, MB lần lượt là khoảng cách từ M đến Ox, Oy.
Theo cách vẽ bằng thước hai lề và từ bài tập 12 ta suy ra: MA = MB (cùng bằng khoảng cách hai lề của thước) hay điểm M cách đều hai cạnh của góc xOy.
Áp dụng định lý 2 suy ra: OM là tia phân giác của góc xOy.
Đúng 0
Bình luận (0)
Cho góc nhọn xOy,Oz là tia phân giác của góc đó.Trên tia Ox lấy điểm A,trên tia Oy lấy điểm B sao cho OA=OB.Gọi I là giao điểm của Oz và AB.a) CM:∆OIA=∆OIB.CM:Oz vuông góc với AB.b)Từ I kẻ IN vuông góc Ox và IM vuông góc Oy(N thuộc Ox,M thuộc Oy).CM: IM=IN.c)CM:góc BIM=góc AIN.d)CM:MN song song AB
a) Xét △OIA và △OIB có:
OA = OB
\(\widehat{AOI}=\widehat{BOI}\)
OI : cạnh chung
Suy ra △OIA = △OIB (c.g.c)
Ta lại có △OAB có OA = OB nên △OAB là tam giác cân tại O
Vì Oz là đường phân giác của △OAB nên Oz đồng thời là đường
cao của △OAB.
Suy ra \(Oz\perp AB\)(*)
b)△INO có \(\widehat{OIN}+\widehat{N}+\widehat{ION}\)= 180o (tổng ba góc của một tam giác)
△IMO có \(\widehat{OI}M+\widehat{M}+\widehat{IOM}\)= 180o (tổng ba góc của một tam giác)
Mà \(\widehat{ION}=\widehat{IOM};\widehat{N}=\widehat{M}=90^o\)
Nên \(\widehat{OIN}=\widehat{OIM}\)
Xét △IMO và △INO có :
\(\widehat{OIN}=\widehat{OIM}\)
IO : cạnh chung
\(\widehat{ION}=\widehat{IOM}\)
Suy ra △IMO = △INO (g.c.g) (**)
Nên IM = IN
c) Từ (*) suy ra \(\widehat{BIO}=\widehat{AIO}=90^o\)
Mặc khác \(\widehat{BIO}=\widehat{BIM}+\widehat{MIO}\)
\(\widehat{AIO}=\widehat{AIN}+\widehat{NIO}\)
Mà\(\widehat{MIO}=\widehat{NIO}\)(từ (**) suy ra)
Nên \(\widehat{BIM}=\widehat{AIN}\)
d)Gọi T là giao điểm của MN và tia Oz
Từ (*) suy ra △AIO vuông tại I và △OTN vuông tại T.
nên \(\widehat{AIO}=\widehat{NTO}=90^o\)
△AIO có: \(\widehat{A}+\widehat{AIO}+\widehat{IOA}\) = 180o(tổng ba góc của một tam giác)
△OTN có: \(\widehat{TNO}+\widehat{NTO}+\widehat{TON}\) = 180o(tổng ba góc của một tam giác)
Mà \(\widehat{AIO}=\widehat{NTO}=90^o\)và \(\widehat{IOA}=\widehat{TON}\)
Suy ra \(\widehat{A}=\widehat{TNO}\)
Nên MN//AB
Đúng 1
Bình luận (3)
Bài 1.7: Qua trung điểm M của đoạn AB vẽ đường thẳng d vuông góc với AB. Trên đường thẳng d lấy điểm K. Chứng minh KM là tia phân giác của góc AKB.Bài 1.8: Cho góc xOy có Ot là tia phân giác. Trên hai tia Ox, Oy lần lượt lấy các điểm M, N sao cho OM ON. Trên tia Ot lấy P bất kì. Chứng minh a) PM PN.b) Khoảng cách từ P đến hai cạnh của góc xOy bằng nhau.
Đọc tiếp
Bài 1.7: Qua trung điểm M của đoạn AB vẽ đường thẳng d vuông góc với AB. Trên đường thẳng d lấy điểm K. Chứng minh KM là tia phân giác của góc AKB.
Bài 1.8: Cho góc xOy có Ot là tia phân giác. Trên hai tia Ox, Oy lần lượt lấy các điểm M, N sao cho OM = ON. Trên tia Ot lấy P bất kì. Chứng minh
a) PM = PN.
b) Khoảng cách từ P đến hai cạnh của góc xOy bằng nhau.
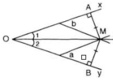
Cho góc xOy = 60°, tia oz là phân giác của góc xOy từ điểm B bất kì trên tia Ox kẻ BH BK lần lượt vuông góc với Oy Oz tại H và K Qua B kẻ đường song song với Oy cắt oz tại M Chứng minh rằng BH = MK
góc BMO=góc HOK=góc BOM
=>ΔBMO cân tại B
=>K là trung điểm của OM
=>OK=KM
Xet ΔHOB vuông tại H và ΔKBO vuông tại K có
BO chung
góc HOB=góc KBO
=>ΔHOB=ΔKBO
=>OK=BH=MK
Đúng 0
Bình luận (1)