cho tam giác ABC có 2 đường cao AD và BE. C/minh tam giác DEC đồng dạng với tam giác ABC

Những câu hỏi liên quan
Cho tam giác ABC nhọn có đường cao AD và BE. chứng minh tam giác DEC đồng dạng với tam giác ABC
Cho tam giác ABC có hai đường cao là AD và BE ( D thuộc BC, E thuộc AC). Chứng minh rằng:
a) tam giác ADC đồng dạng tam giác BEC.
b) AC.EC=BC.DC
c) tam giác DEC đồng dạng tam giác ABC.
xét tam giác EBC và tam giác DAC có :
góc C chung
góc ADC = góc BEC = 90
=> tam giác EBC ~ tam giác DAC (g - g)
Đúng 0
Bình luận (0)
Tam giác ABC có hai đường cao là AD và BE (D thuộc BC và E thuộc AC). Chứng minh hai tam giác DEC và ABC là hai tam giác đồng dạng.
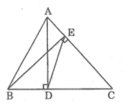
Xét △ ADC và △ BEC, ta có:
∠ (ADC) = ∠ (BEC) = 90 0
∠ C chung
Suy ra: △ ADC đồng dạng △ BEC (g.g)
Suy ra: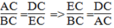 ⇒ ECBC = DCAC
⇒ ECBC = DCAC
Xét △ DEC và △ ABC ta có:
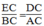
∠ C chung
Vậy △ DEC đồng dạng △ ABC (c.g.c)
Đúng 0
Bình luận (0)
cho tam giác ABC có đường cao AD,BE.Chứng minh tam giác DEC đồng dạng tam giác ABC
Tam giác ABC có hai đường cao là AD và BE (D thuộc BC, E thuộc AC). Chứng minh hai tam giác DEC và ABC là hai tam giác đồng dạng ?
cho tam giác abc nhọn các đường cao ad và be cắt nhau tại h. qua a kẻ đường thẳng song song với bc, qua b kẻ đường thảng song song với ad, chứng cắt nhau tại m. a) tứ giác ambd là hình gì? chứng minh b) chứng minh tam giác ahe đồng dạng với tam giác bec, tam giác dec đồng dạng với tam giác abc
Cho tam giác ABC nhọn, có BE,AD là đường cao cắt ở H a) CM tam giác CDA đồng dạng tam giác CEB b) CM HA.HD=HB.HE c) CM tam giác ABC đồng dạng tam giác DEC d) Qua D kẻ đường thẳng vuông góc DE cắt BE tại M. CM góc ABC= góc EMD
a: Xét ΔCDA vuông tại D và ΔCEB vuông tại E có
góc C chung
Do đó: ΔCDA\(\sim\)ΔCEB
b: Xét ΔHEA vuông tại E và ΔHDB vuông tại D có
\(\widehat{AHE}=\widehat{BHD}\)
Do đó: ΔHEA\(\sim\)ΔHDB
Suy ra: HE/HD=HA/HB
hay \(HE\cdot HB=HD\cdot HA\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có ba đường cao AD, BE và CF cắt nhau tại H. a, Chứng minh: AExAC = AF×AB b, Chứng minh: tam giác AEF đồng dạng với tam giác ABC ;tam giác BFD đồng dạng với tam giác BCA c, Chứng minh tam giác CFD đồng dạng tam giác CBH
a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
góc A chung
=>ΔABE đồng dạng với ΔACF
=>AB/AC=AE/AF
=>AB*AF=AE*AC: AB/AE=AC/AF
b: Xet ΔABC và ΔAEF có
AB/AE=AC/AF
góc BAC chung
=>ΔABC đồng dạng với ΔAEF
góc BFC=góc BDA=90 độ
mà góc B chung
nên ΔBFC đồng dạng với ΔBDA
=>BF/BD=BC/BA
=>BF/BC=BD/BA
=>ΔBFD đồng dạng với ΔBCA
Đúng 2
Bình luận (0)
Bài: Cho tam giác ABC nhọn với các đường cao AD, BE (D thuộc BC; E thuộc AC). Chứng minh tam giác DEC đồng dạng với tam giác ABC
- Bài này hơi khó, giúp mình nhé, cám ơn !


















