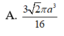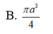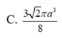Cho hình bình hành ABCD có hai đỉnh A,B cố định, còn đỉnh C chạy trên một đường tròn (O;R). Tìm quỹ tích đỉnh D khi C thay đổi .
Cho hình bình hành ABCD có đỉnh A cố định, BD có độ dài ko đổi bằng 2a, còn A,B,D nằm trên 1 đường tròn cố định tâm O, bán kính R.Tìm Quỹ tích điểm C
Cho hình bình hành ABCD có đỉnh A cố định, BD có độ dài ko đổi bằng 2a, còn A,B,D nằm trên 1 đường tròn cố định tâm O, bán kính R.Tìm Quỹ tích điểm C
Sử dụng phép tịnh tiến nha
Mà tìm quỹ tích C trong trường hợp nào hã bạn ???????????
Cho có hai đỉnh B, C cố định còn đỉnh A chạy trên một đường tròn ( O:R ). Tìm quỹ tích trọng tâm G của ∆ A B C
A. Đường tròn O ; 1 3 R là ảnh của đường tròn ( O;R ) qua phép vị tự tâm I tỉ số k = 1 3
B. Đường tròn O ; 2 3 R là ảnh của đường tròn ( O;R ) qua phép vị tự tâm I tỉ số k = 2 3
C. Đường tròn O ; 4 3 R là ảnh của đường tròn ( O;R ) qua phép vị tự tâm I tỉ số k = 4 3
D. Đường tròn ( O;3R ) là ảnh của đường tròn ( O;R ) qua phép vị tự tâm I tỉ số k = 3
Gọi I là trung điểm BC. Khi đó I G = 1 3 I A ⇒ G = V I ; 1 3
Mà A ∈ O ; R nên quỹ tích trọng tâm G của ∆ A B C là đường tròn O ; 1 3 R là ảnh của đường tròn ( O;R ), qua phép vị tự tâm I tỉ số k = 1 3
Đáp án A
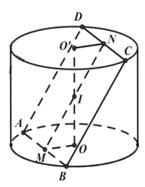
Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ một góc 45°. Tính thể tích của khối trụ.
A. πa 3 2 16
B. πa 3 2 4
C. πa 3 2 2
D. 3 πa 3 2 16
Đáp án D
Gọi M, N lần lượt là trung điểm AB và CD.
Khi đó OM ⊥ AB và O’N ⊥ CD
Gọi I là giao điểm của MN và OO’
Đặt R = OA và h = OO’. Khi đó ΔIOM vuông cân tại O nên:
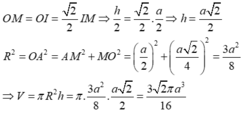
Cho điểm A cố định trên đường tròn (O) và một điểm C di động trên đường tròn đó. Dựng hình vuông ABCD (thứ tự các đỉnh theo chiều dương). Khi đó quỹ tích điểm D là ảnh của đường tròn (O) qua phép biến hình F có được bằng cách thực hiện liên tiếp:
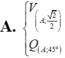
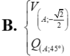
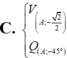
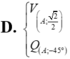
Cho điểm A cố định trên đường tròn (O) và một điểm C di động trên đường tròn đó. Dựng hình vuông ABCD (thứ tự các đỉnh theo chiều dương). Khi đó quỹ tích điểm D là ảnh của đường tròn (O) qua phép biến hình F có được bằng cách thực hiện liên tiếp:
A. V A ; 2 2 Q A ; 45 °
B. V A ; − 2 2 Q A ; 45 °
C. V A ; − 2 2 Q A ; − 45 °
D. V A ; 2 2 Q A ; − 45 °
Cho điểm A cố định trên đường tròn (O) và một điểm C di động trên đường tròn đó. Dựng hình vuông ABCD (thứ tự các đỉnh theo chiều dương). Khi đó quỹ tích điểm D là ảnh của đường tròn (O) qua phép biến hình F có được bằng cách thực hiện liên tiếp:
A. V A ; 2 2 Q A , 45 °
B. V A ; - 2 2 Q A , 45 °
C. V A ; - 2 2 Q A , - 45 °
D. V A ; 2 2 Q A , - 45 °
D
Đáp án A.
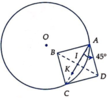
V A ; 2 2 A = K ⇒ K nằm giữa AC và AK = AD
Từ hình vẽ Q A ; 45 ° ( K ) = D
Cho một hình trụ tròn xoay và hình vuông ABCD cạnh a có hai đỉnh liên tiếp A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ góc 45 ° . Thể tích của hình trụ bằng:
A. 3 2 π a 3 16
B. π a 3 4
C. 3 2 π a 3 8
D. 2 π a 3 16
Cho một hình trụ tròn xoay và hình vuông (ABCD) cạnh a có hai đỉnh liên tiếp A, B nằm trên đường tròn đáy thứ nhất của hình trụ, hai đỉnh còn lại nằm trên đường tròn đáy thứ hai của hình trụ. Mặt phẳng (ABCD) tạo với đáy hình trụ góc . Thể tích của hình trụ bằng