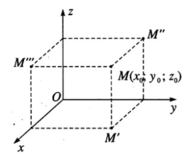
Gọi M’, M’’, M’’’ lần lượt là hình chiếu vuông góc của điểm M trên các mặt phẳng (Oxy), (Oyz), (Ozx).

Ta có:

     • M’( x 0 ;  y 0 ; 0)

     • M’’ (0;  y 0 ;  z 0 )

     • M’’’( x 0 ; 0;  z 0 )

Đáp án A

Vẽ D H ⊥ A ' C .

Ta có: ∆ A ' D C = ∆ A ' B C  (c.g.c) ⇒ B H = H D  

⇒ ∆ B H C = ∆ D H C  (c.c.c)  ⇒ B H C ^ = 90 °

Vậy góc giữa hai mặt phẳng (BA'C) và (DA'C) là góc  B H D ^

Trong ∆ A ' D C  vuông tại D

⇒ D H = D A ' . D C A ' C = a 2 3 = a 6 3

Trong ∆ H B D  có  cos   B H D ^ = B H 2 + H D 2 - B D 2 2 B H . H D = - 1 2

Suy ra góc giữa hai mặt phẳng (BA'C) và (DA'C) là góc 60°.

Đáp án C.

Gọi C là trọng tâm của tam giác ABC ⇒ G 2 ; 1 ; 3  

Khi đó M A → + M B → + M C → = 3 M G → + G A → + G B → + G C → ⏟ 0 = 3 M G → = 3 M G . 

Suy ra M G m i n ⇔  M là hình chiếu của G trên mp (Oxy) ⇒ M 2 ; 1 ; 0 .

Gọi \(M\left(2;y_M\right)\) là tiếp điểm của (C):

\(\Leftrightarrow2^2+y_M^2-12+2y_M=0\)

\(\Leftrightarrow y_M^2+2y_M-8=0\)

\(\Leftrightarrow\left[{}\begin{matrix}y_M=2\\y_M=-4\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}M\left(2;2\right)\\M\left(2;-4\right)\end{matrix}\right.\)

* Với M(2;2)

Ta có: \(\overrightarrow{u}=\overrightarrow{IE}=\left(-1;3\right)\Rightarrow\overrightarrow{n}=\left(3;1\right)\)

\(\Rightarrow\left(D\right):3x+y-8=0\)

* Với M(2; -4)

Ta có: \(\overrightarrow{u}=\overrightarrow{IE}=\left(-1;-3\right)\Rightarrow\overrightarrow{n}=\left(-3;1\right)\)

\(\Rightarrow\left(D\right):-3x+y+4=0\)

Đáp án C