Xét vị trí tương đối của các đường thẳng sau đây:d1 :12x – 6y + 10 0 ; d2 :
Đọc tiếp
Xét vị trí tương đối của các đường thẳng sau đây:
d1 :12x – 6y + 10 = 0 ; d2 :
Những câu hỏi liên quan
Xét vị trí tương đối của đường thẳng Δ: x – 2y + 1 = 0 với mỗi đường thẳng sau:
d1: -3x + 6y – 3 = 0;
d2: y = -2x;
d3: 2x + 5 = 4y.
Xét Δ và d1, hệ phương trình: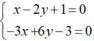 
có vô số nghiệm (do các hệ số của chúng tỉ lệ nên Δ ≡ d1.
Xét Δ và d2, hệ phương trình: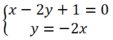 
có nghiệm duy nhất (-1/5; 2/5) nên
Δ cắt d2 tại điểm M(-1/5; 2/5).
Xét Δ và d3, hệ phương trình: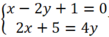 
vô nghiệm
Vậy Δ // d3
Đúng 0
Bình luận (0)
xác định vị trí tương đối của 2 đường thẳng sau đây △1: x-2y+1=0; △2: -3x+6y-10=0
Xác định vị trí tương đối của 2 đường thẳng sau đây: (d1): x- 2y+ 10 và (d2): -3x+ 6y-1 0 . A. Song song. B. Trùng nhau. C. Vuông góc nhau. D. Cắt nhau.
Đọc tiếp
Xác định vị trí tương đối của 2 đường thẳng sau đây: (d1): x- 2y+ 1=0 và (d2): -3x+ 6y-1 =0 .
A. Song song.
B. Trùng nhau.
C. Vuông góc nhau.
D. Cắt nhau.
Đường thẳng (d1) có vtpt 
và
d2 có vtpt 
Hai đường thẳng này có
nên hai đường thẳng này song song với nhau.
Chọn A.
Đúng 0
Bình luận (0)
Xét vị trí tương đối của các cặp mặt phẳng cho bởi phương trình tổng quát sau đây: ( α 1 ): 3x − 2y − 3z + 5 = 0, ( α ' 1 ): 9x − 6y − 9z – 5 = 0
Xét vị trí tương đối của các cặp đường thẳng d1 và d2 sau đây:
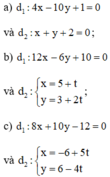
Cách 1: Dựa vào số nghiệm của hệ phương trình:
a) Xét hệ phương trình
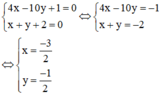
Hệ phương trình có nghiệm duy nhất nên (d1) cắt (d2).
b) Xét hệ phương trình
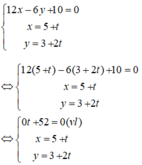
Hệ phương trình trên vô nghiệm nên hai đường thẳng trên song song.
c) Xét hệ phương trình
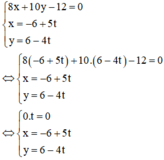
Hệ phương trình trên có vô số nghiệm nên hai đường thẳng trùng nhau.
Cách 2: Dựa vào vị trí tương đối của các vectơ chỉ phương (hoặc vectơ pháp tuyến).
a) d1 nhận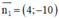 
là một vectơ pháp tuyến
d2 nhận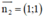 
là 1 vtpt
Nhận thấy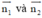 
không cùng phương nên d1 cắt d2.
b) d1 nhận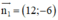 
là 1 vtpt ⇒ d1 nhận 
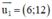là 1 vtcp
d2 nhận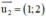 
là 1 vtcp.
Nhận thấy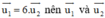 
cùng phương
⇒ d1 và d2 song song hoặc trùng nhau.
Xét điểm M(5;3) có:
M(5; 3) ∈ d2
12.5 – 6.3 + 10 = 52 ≠ 0 nên M(5; 3) ∉ d1.
Vậy d1 và d2 song song.
c) d1 nhận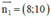 
là 1 vtpt ⇒ d1 nhận 
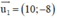là 1 vtcp.
d2 nhận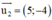 
là 1 vtcp.
Nhận thấy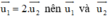 
cùng phương
⇒ d1 và d2 song song hoặc trùng nhau.
Xét M(–6; 6) ∈ d2; M(–6; 6) ∈ d1 (Vì 8.(–6) + 10.6 – 12 = 0)
⇒ d1 và d2 trùng nhau.
Đúng 0
Bình luận (0)
Xét vị trí tương đối của đường thẳng d với mặt phẳng (α) trong các trường hợp sau:
x
1
+
t
y
2
-
t
z
1...
Đọc tiếp
Xét vị trí tương đối của đường thẳng d với mặt phẳng (α) trong các trường hợp sau: x = 1 + t y = 2 - t z = 1 + 2 t α : x + 3 y + z + 1 = 0
Giao điểm (nếu có) của đường thẳng (d) và mp(α ) là nghiệm hệ phương trình:
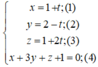
Thay (1); (2); (3) vào (4) ta được:
1 + t + 3(2 – t) + 1 + 2t + 1 = 0
⇔ 0t + 9 = 0
Phương trình vô nghiệm
⇒ (d) không cắt (α).
Đúng 0
Bình luận (0)
Xét vị trí tương đối của đường thẳng d với mặt phẳng (α) trong các trường hợp sau:
d
:
x
1
+
t
y
1
+
2
t
z...
Đọc tiếp
Xét vị trí tương đối của đường thẳng d với mặt phẳng (α) trong các trường hợp sau:
d : x = 1 + t y = 1 + 2 t z = 2 - 3 t α : x + y + z - 4 = 0
Giao điểm (nếu có) của đường thẳng (d) và mp(α) là nghiệm hệ phương trình:
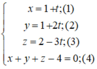
Thay (1); (2); (3) vào (4) ta được:
1 + t + 1 + 2t + 2 – 3t – 4 = 0
⇔ 0t = 0
Phương trình có vô số nghiệm
⇒ (d) ⊂ (α)
hay (d) cắt (α) tại vô số điểm.
Đúng 0
Bình luận (0)
Xét vị trí tương đối của đường thẳng d với mặt phẳng (
α
) trong các trường hợp sau:
d
:
x
2
-
t
y
t
z...
Đọc tiếp
Xét vị trí tương đối của đường thẳng d với mặt phẳng ( α ) trong các trường hợp sau:
d : x = 2 - t y = t z = 2 + t và ( α ): x + z + 5 = 0
Thay x, y, z trong phương trình tham số của d vào phương trình tổng quát của ( α ) ta được: (2 – t) +(2 + t) + 5 = 0 ⇔ 0t = -9
Phương trình vô nghiệm, vậy đường thẳng d song song với ( α )
Đúng 0
Bình luận (0)
Xét vị trí tương đối của đường thẳng d với mặt phẳng (α) trong các trường hợp sau:
d
:
x
12
+
4
t
y
9
+
3
t...
Đọc tiếp
Xét vị trí tương đối của đường thẳng d với mặt phẳng (α) trong các trường hợp sau: d : x = 12 + 4 t y = 9 + 3 t z = 1 + t α : 3 x + 5 y - z - 2 = 0
Giao điểm (nếu có) của đường thẳng (d) và mp(α ) là nghiệm hệ phương trình:
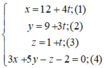
Thay (1); (2); (3) vào (4) ta được:
3(12 + 4t) + 5(9 + 3t) – (1 + t) – 2 = 0
⇔ 36 + 12t + 45 + 15t – 1 – t – 2 = 0
⇔ 26t + 78 = 0
⇔ t = -3
Vậy (d) cắt (α) tại một điểm M(0 ; 0 ; -2).
Đúng 0
Bình luận (0)
Xét vị trí tương đối của đường thẳng d với mặt phẳng (
α
) trong các trường hợp sau:
d
:
x
t
y
1
+
2
t...
Đọc tiếp
Xét vị trí tương đối của đường thẳng d với mặt phẳng ( α ) trong các trường hợp sau:
d : x = t y = 1 + 2 t z = 1 - t và ( α ): x + 2y + z - 3 = 0
Thay x, y, z trong phương trình tham số của đường thẳng d vào phương trình tổng quát của mặt phẳng ( α ) ta được: t + 2(1 + 2t) + (1 – t) – 3 = 0
⇔ 4t = 0 ⇔ t = 0
Vậy đường thẳng d cắt mặt phẳng ( α ) tại M 0 (0; 1; 1)
Đúng 0
Bình luận (0)