2> Tìm tọa độ hình chiếu vuông góc của A lên D trong các tập hợp sau :
a> A (1; 2) , D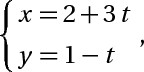
b> A(1,-1) , D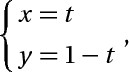
c> A(2,-3) , D: 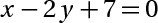
Trong không gian vỏi hệ tọa độ Oxỵz, cho đường thẳng △ : x + 1 2 = y - 2 - 1 = z 2 . Tìm tọa độ điểm H là hình chiếu vuông góc của điểm A(2; -3; 1) lên △
A . H ( - 3 ; - 1 ; - 2 )
B . H ( - 1 ; - 2 ; 0 )
C . H ( 3 ; - 4 ; 4 )
D . H ( 1 ; - 3 ; 2 )
Trong không gian vỏi hệ tọa độ Oxỵz, cho đường thẳng ∆ : x + 1 2 = y + 2 - 1 = z 2 . Tìm tọa độ điểm H là hình chiếu vuông góc của điểm A(2;-3;1) lên ∆ .
A. H(-3;-1;-2)
B. H(-1;-2;0)
C. H(3;-4;4)
D. H(1;-3;2)
Đáp án D.
![]()
Vì H là hình chiếu vuông góc của A lên đường thẳng ∆
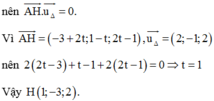
Trong không gian với hệ trục tọa độ Oxyz, cho điểm M(1;-2;3). Tìm tọa độ điểm A là hình chiếu vuông góc của M lên mặt phẳng (Oyz)
A. A(1;-2;3)
B. A(1;-2;0)
C. A(1;0;3)
D. A(0;-2;3)
Trong mặt phẳng tọa độ Oxy, cho parabol (P):y=x2 . Gọi A, B là hai điểm trên parabol có
hoành độ tương ứng là 1 và 2. Tìm tọa độ hình chiếu vuông góc của gốc tọa độ O lên đường
thẳng AB.
Thay x=1 vào (P), ta được:
\(y=1^2=1\)
Thay x=2 vào (P), ta được:
\(y=2^2=4\)
vậy: A(1;1); B(2;4)
Gọi H là tọa độ của hình chiếu vuông góc kẻ từ O xuống AB
O(0;0); H(x;y); A(1;1); B(2;4)
\(\overrightarrow{OH}=\left(x;y\right);\overrightarrow{AB}=\left(1;3\right)\)
Vì OH vuông góc với AB nên \(x\cdot1+y\cdot3=0\)
=>x+3y=0
Ta có: \(\overrightarrow{AH}=\left(x-1;y-1\right);\overrightarrow{AB}=\left(1;3\right)\)
mà A,H,B thẳng hàng
nên \(\dfrac{x-1}{1}=\dfrac{y-1}{3}\)
=>3x-3=y-1
=>3x-y=2(2)
Từ (1) và (2) ta có hệ phương trình:
\(\left\{{}\begin{matrix}3x-y=2\\x+3y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}9x-3y=6\\x+3y=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}10x=6\\x+3y=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{3}{5}\\3y=-x=-\dfrac{3}{5}\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x=\dfrac{3}{5}\\y=-\dfrac{1}{5}\end{matrix}\right.\)
Vậy: \(H\left(\dfrac{3}{5};-\dfrac{1}{5}\right)\)
Trong không gian với hệ trục tọa độ Oxyz, gọi H là hình chiếu vuông góc của điểm A(-3;-1;-1) lên mặt phẳng (P): 2x + y + z - 4 = 0. Tìm tọa độ điểm H
A. H(2;0;0)
B. H(1;2;0)
C. H(1;1;1)
D. H ( 1 2 ; 1 ; 2 )
Trong không gian với hệ tọa độ Oxyz, cho điểm A ( 1 ; 2 ; 3 ) và cho đường thẳng d có phương trình x − 2 2 = y + 2 − 1 = z − 3 1 . Tìm tọa độ hình chiếu vuông góc H của A trên d.
A. H(0;1;2)
B. H(0;-1;2)
C. H(1;1;1)
D. H(-3;1;4)
Trong không gian với hệ tọa độ Oxyz,
cho điểm A(3;-2;5) và đường thẳng (d): x = - 8 + 4 t y = 5 - 2 t z = t .
Tọa độ hình chiếu vuông góc của điểm A
lên đường thẳng (d).
![]()
![]()
![]()
![]()
Đáp án A
Xét yếu tố vuông góc nhập
![]()
hoành độ, tung độ, cao độ của các đáp án.
Ta thấy chỉ có đáp án (4; -1; 3) cho kết quả
bằng 0.
Trong không gian với hệ tọa độ Oxyz , cho điểm A 3 ; − 2 ; 5 và đường thẳng (d) x = − 8 + 4 t y = 5 − 2 t z = t . Tọa độ hình chiếu vuông góc của điểm (A) lên đường thẳng (d).
A. 4 ; − 1 ; 3
B. − 4 ; 1 ; − 3
C. 4 ; − 1 ; − 3
D. - 4 ; − 1 ; − 3
Trong không gian với hệ tọa độ Oxyz cho điểm A(4 ;-3 ;2). Hình chiếu vuông góc của A lên các trục tọa độ Ox, Oy, Oz theo thứ tự lần lượt là M, N, P. Phương trình mặt phẳng (MNP) là
A. 4x - 3y + 2z - 5 = 0
B. 3x - 4y + 6z - 12 = 0
C. 2x - 3y + 4z - 1 = 0
D. x 4 - y 3 + z 2 + 1 = 0
Từ giả thiết, ta có M(4 ;0 ;0), N(0 ;-3 ;0), P(0 ;0 ;2)
Phương trình mặt phẳng (MNP) theo đoạn chắn là
![]()
Chọn B.
Trong mặt phẳng hệ trục tọa độ Oxy, cho tam giác ABC nội tiếp đường tròn tâm I; E (1/2;1/2) là trung điểm AB. H (4/5;-22/5) là tọa độ hình chiếu vuông góc của A lên CI. Ptdt BC : x+y-4=0. Tìm tọa độ A,B,C