Cho đa thức: P(x) = ax4 + bx3 + cx2 + dx + e nguyên với mọi x
C/M : a, b, c, d, e nguyên
1. Cho đa thức f(x)ϵZ[x]
f(x)=ax4+bx3+cx2+dx+e với a, b, c, d, e là các số lẻ.
Cm đa thức không có nghiệm hữu tỉ
Cho đa thức P(x)=ax4+bx3+cx2+dx+e, biết P(1)=P(-1), P(2)=P(-2).
Chứng minh P(x)=P(-x) với mọi x
( giải giúp với ạ? )
Bài 1: Tìm đa thức M biết : M-3xyz+5x2-7xy+9=6x2+xyz+2xy+3-y2
Bài 2: Cho đa thức P(x)= ax4+bx3+cx2+dx+e, biết P(1)=P(-1) , P(2)=P(-2).
Chứng minh P(x)=P(-x) với mọi x.
( giúp mình với :< )
Bài 1:
\(M=6x^2+xyz+2xy+3-y^2+3xyz-5x^2+7xy-9\)
\(=x^2+4xyz+9xy-y^2-6\)
Bài 1: Tìm đa thức M biết : M-3xyz+5x2-7xy+9=6x2+xyz+2xy+3-y2
Bài 2: Chứng minh đa thức sau vô nghiệm :
a)ax2+2x+3 b)x2+4x+6
Bài 3: Cho đa thức P(x)= ax4+bx3+cx2+dx+e, biết P(1)=P(-1) , P(2)=P(-2).
Chứng minh P(x)=P(-x) với mọi x
( giúp mình nha cảm ơn mọi người aa<3 )
Bài 2:
a: Sửa đề: \(x^2+2x+3\)
Đặt \(x^2+2x+3=0\)
\(\Delta=2^2-4\cdot1\cdot3=4-12=-8< 0\)
Do đó: Phương trình vô nghiệm
b: Đặt \(x^2+4x+6=0\)
\(\Leftrightarrow x^2+4x+4+2=0\)
\(\Leftrightarrow\left(x+2\right)^2+2=0\)(vô lý)
Biết rằng đồ thị hàm số y = f ( x ) = ax 4 + bx 3 + cx 2 + dx + e ( a ≠ 0 ; b ≠ 0 ) cắt trục Ox tại 4 điểm phân biệt. Khi đó đồ thị hàm số y = g ( x ) = ( 4 ax 3 + 3 bx 2 + 2 cx + d ) 2 - 2 ( 6 ax 2 + 3 bx + c ) . ( ax 4 + bx 3 + cx 2 + dx + e ) cắt trục Ox tại bao nhiêu điểm?
A. 0
B. 4
C. 2
D. 6
Ta có
![]()
Đồ thị hàm số ![]() cắt trục hoành tại bốn điểm phân biệt bên phương trình
cắt trục hoành tại bốn điểm phân biệt bên phương trình ![]() , với
, với ![]() là các nghiệm.
là các nghiệm.
Suy ra
![]()
![]()
![]()
![]()
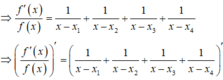
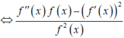
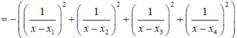
Nếu ![]() với
với ![]() thì
thì ![]() ,
, ![]()
![]() .
.
Nếu ![]() thì
thì 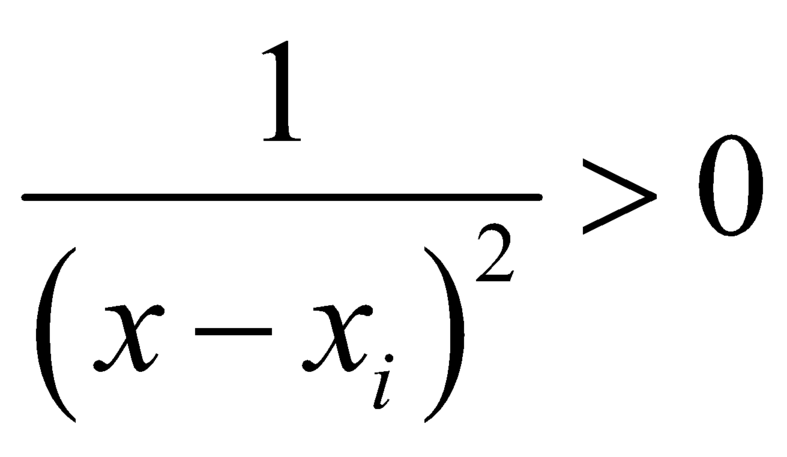 ,
, ![]() .
.
Suy ra ![]()
![]() .
.
Vậy phương trình ![]() vô nghiệm hay phương trình
vô nghiệm hay phương trình ![]() vô nghiệm.
vô nghiệm.
Do đó, số giao điểm của đồ thị hàm số và trục hoành là 0
Đáp án A
Cho hàm số f(x) = a x 4 + b x 3 + c x 2 + d x + e , với a,b,c,d,e ∈ ℝ . Hàm số y = f'(x) có đồ thị như hình vẽ. Trong các khẳng định sau, khẳng định nào đúng?
A. a + b + c + d < 0.
B. a + c < b + d
C. a + c > 0
D. d + b - c > 0
Chọn C
Ta có: ![]()
Dựa vào đồ thị:
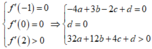

![]()
Dựa vào đồ thị, ta cũng có: ![]()
Từ (1),(2) suy ra a + c > 4a + c > 0.
Cho hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e , ( a , b , c , d , e ∈ ℝ ) Hàm y=f'(x) có bảng xét dấu như sau:
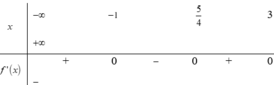
Số nghiệm của phương trình f(x)=e là
A. 1
B. 0
C. 2
D. 3
Cho hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e có bảng biến thiên như hình vẽ sau
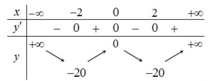
Có bao nhiêu số nguyên dương m để hàm số y=|f(x)+m| có 7 điểm cực trị.
A. 0.
B. 21.
C. 18.
D. 19.
Hình vẽ bên là đồ thị của hàm số f ( x ) = a x 4 + b x 3 + c x 2 + d x + e .
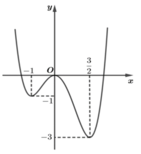
Hỏi có bao nhiêu m nguyên để phương trình f x = m có ít nhất ba nghiệm phân biệt?
A. 1.
B. 2.
C. 3.
D. 4.
Từ đồ thị hàm số (C): y = f(x) ta suy ra đồ thị hàm số (C'): y = f(|x|) như sau:
+) Giữ nguyên phần đồ thị (C) trên miền x ≥ 0 , (kí hiệu phần đồ thị này là C 1 ).
+) Bỏ phần đồ thị (C) ở bên trái trục Oy.
+) Lấy đối xứng C 1 qua trục Oy, (kí hiệu phần đồ thị này là C 2 ).
Khi đó đồ thị của hàm số y = f(|x|) là hợp của hai phần đồ thị C 1 và C 2 .
Ta có đồ thị của hàm số y = f(|x|) như hình vẽ dưới đây:
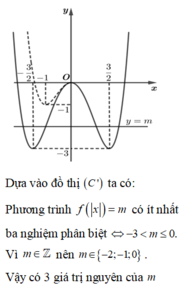
Chọn C
Biết rằng đồ thị hàm số y = f t = a x 4 + b x 3 + c x 2 + d x + e , a , b , c , d ∈ ℝ ; a ≠ 0 , b ≠ 0 cắt trục hoành Ox tại 4 điểm phân biệt. Khi đó đồ thị hàm số y = g x = 4 a x 3 + 3 b x 2 + 2 c x + d 2 - 2 6 a x 2 + 3 b x + c . a x 4 + b x 3 + c x 2 + d x + e cắt trục hoành Ox tại bao nhiêu điểm?
A. 6
B. 0
C. 4
D. 2
Đáp án B
Giả thiết
![]()
Đặt
![]()
thì
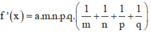
Và
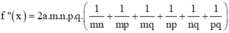
Khi đó, phương trình
![]() (vô nghiệm)
(vô nghiệm)
Vậy đồ thị hàm số y = g(x) không cắt trục hoành.