Sủa đề : CM \(A=\frac{2ax-2x-3y+3ay}{4ax+4x+6y+6ay}\) ko phụ thuộc vào biếnx;y :

Ta có : \(\frac{2ax-2x-3y+3ay}{4ax+4x+6y+6xy}=\frac{a\left(2x+3y\right)-\left(2x+3y\right)}{2a\left(2x+3y\right)+2\left(2x+3y\right)}=\frac{\left(a-1\right)\left(2x+3y\right)}{\left(2a+2\right)\left(2x+3y\right)}=\frac{a-1}{2a+2}\)

Biểu thức sau khi dút gọn ko chứa biến của x;y nên A ko phụ thuộc vào biến x;y (đpcm)

Ko sai đâu, mình làm tắt quá nên bạn ko hiểu thoy :))

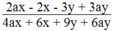xác định khi 4ax + 6x + 9y + 6ay ≠ 0

⇒ 2x(2a + 3) + 3y(2a + 3) = (2a + 3)(2x + 3y)  ≠  0

Ta có: 2a + 3  ≠  0 ⇒ a  ≠  - 3/2 ; 2x + 3y  ≠  0 ⇒ x  ≠  - 3/2 y

Điều kiện: x  ≠  - 3/2 y và a  ≠  - 3/2

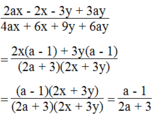
Vậy biểu thức không phụ thuộc vào x, y.

a) \(\frac{\left(x+a\right)^2-x^2}{2x+a}=\frac{x^2+2xa+a^2-x^2}{2x+a}=\frac{2ax+a^2}{2x+a}=\frac{a\left(2x+a\right)}{2x+a}=a\)

b) \(\frac{x^2-y^2}{axy-ax^2-ay^2-axy}=\frac{x^2-y^2}{-a\left(x^2+y^2\right)}\) =>cần phụ thuộc vào x,y (Không thì đề sai)

c) \(\frac{2ax-2x-3y+3ay}{4ax+6x+9y+6ay}=\frac{2x\left(a-1\right)+3y\left(a-1\right)}{2x\left(a+3\right)+3y\left(a+3\right)}=\frac{\left(2x+3y\right)\left(a-1\right)}{\left(2x+3y\right)\left(a+3\right)}=\frac{a-1}{a+3}\)

Bạn xem đề câu b và c nhé..... C tớ có sửa rồi nhưng không biết đúng hay sai

a) Ta có : \(\frac{x^2-y^2}{(x+y)(ay-ax)}\) = \(\frac{(x-y)(x+y)}{(x+y).a(y-x)}\)

= \(\frac{(x-y)(x+y)}{-a(x-y)(x+y)}\)

= \(\frac{-1}{a}\)

Vì \(\frac{x^2-y^2}{(x+y)(ay-ax)}\) = \(\frac{-1}{a}\) Nên giá trị của \(\frac{x^2-y^2}{(x+y)(ay-ax)}\) không phụ thuộc vào biến x

b) Xem lại đề bài nhé Đề bài sai chăng ?!

bạn xem lại đề thử nhé

\(A=\frac{ac+bx+ax+bc}{ay+2bx+2ax+by}=\frac{a\left(c+x\right)+b\left(c+x\right)}{a\left(y+2x\right)+b\left(y+2x\right)}=\frac{\left(c+x\right)\left(a+b\right)}{\left(y+2x\right)\left(a+b\right)}\)

Do \(a\ne-b\Rightarrow a+b\ne0\Rightarrow\)\(A=\frac{c+x}{y+2x}\), giá trị không phụ thuộc vào a; b (đpcm)

a, (4x+4y)+(by+bx)= 4(x+y)+b(x+y)=(x+y)(4+b)

b, ( 2x²+xy)-(2x+y)= x(2x+y)-(2x+y)=(2x+y)(x-1)

c, (3ax-2bx)-(6ay-4by)= x(3a-2b)-2y(3a-2b)=(3a-2b)(x-2y)

d, (ma+na-pa)-(mb+nb-pb)= a(m+n+p)-b(m+n-p)=(m+n+p)(a-b)

a) 4x+bx+by+4y                b)2x²+xy-2x-y                c)3ax-2bx-6ay+4by                          d)ma-mb+na-nb-pa+pb

=x(4+b)+y(b+4)                 =2x(x-1)+y(x-1)              =3ax-6ay-2bx+4by                            =m(a-b)+n(a-b)-p(a-b)

=(x+y)(b+4)                      =(x-1)(2x+1)                   =3a(x-2y)-2b(x-2y)=(3a-2b)(x-2y)        =(a-b)(m+n-p)