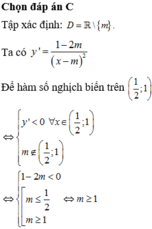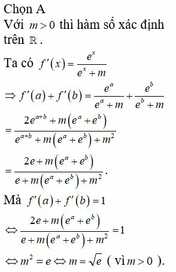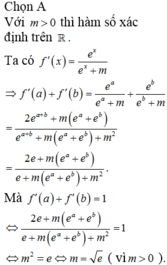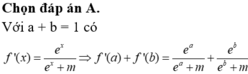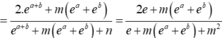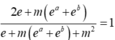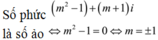cho số thực m<0 tùy theo giá trị của m. hãy tìm (\(-\infty\);m) giao với (\(\frac{1}{3m};+\infty\))

Những câu hỏi liên quan
Cho hàm số
y
2
x
-
1
x
-
m
, m là tham số thực. Tìm tất cả giá trị thực của m để hàm số nghịch biến trên khoảng A.
1
2
m
≤
1
B.
m
1
2
C.
m
≥...
Đọc tiếp
Cho hàm số y = 2 x - 1 x - m , m là tham số thực. Tìm tất cả giá trị thực của m để hàm số nghịch biến trên khoảng
A. 1 2 < m ≤ 1
B. m > 1 2
C. m ≥ 1
D. m ≥ 1 2
Cho hàm số
y
2
x
-
1
x
-
m
, m là tham số thực. Tìm tất cả giá trị thực của m để hàm số nghịch biến trên khoảng
1
2
;
1
? A.
1
2
m
⩽...
Đọc tiếp
Cho hàm số y = 2 x - 1 x - m , m là tham số thực. Tìm tất cả giá trị thực của m để hàm số nghịch biến trên khoảng 1 2 ; 1 ?
A. 1 2 < m ⩽ 1 .
B. m > 1 2 .
C. m ⩾ 1 .
D. m ⩾ 1 2 .
Cho hàm số
y
m
3
x
3
+
m
-
2
x
2
+
m
-
1
x
, với m là tham số thực. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đạt cực đại tại điểm
x
1
và đạt cực tiểu...
Đọc tiếp
Cho hàm số y = m 3 x 3 + m - 2 x 2 + m - 1 x , với m là tham số thực. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đạt cực đại tại điểm x 1 và đạt cực tiểu tại điểm x 2 thỏa mãn x 1 < x 2
A. 0 < m < 4 3
B. m ≤ 0
C. 5 4 < m < 4 3
D. Không tồn tại m
Chọn A.
Phương pháp : Sử dụng đạo hàm và đặc trưng cực trị hàm số đa thức bậc ba.
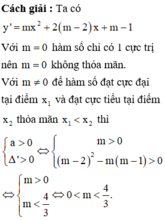
Đúng 0
Bình luận (0)
Cho hàm số
f
x
ln
e
x
+
m
. Có bao nhiêu số thực dương m để
f
a
+
f
b
1
với mọi số thực a,b thỏa m...
Đọc tiếp
Cho hàm số f x = ln e x + m . Có bao nhiêu số thực dương m để f ' a + f ' b = 1 với mọi số thực a,b thỏa mãn a + b = 1
A.1
B.2
C. Vô số
D.0
Cho hàm số
y
m
3
x
3
+
(
m
-
2
)
x
2
+
(
m
-
1
)
x
+
2
, với
m
là tham số thực. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số đạt cực đại tại điểm
x
1
và đạt...
Đọc tiếp
Cho hàm số y = m 3 x 3 + ( m - 2 ) x 2 + ( m - 1 ) x + 2 , với m là tham số thực. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đạt cực đại tại điểm x 1 và đạt cực tiểu tại điểm x 2 thỏa mãn x 1 < x 2
A. 0 < m < 4 3
B. m ≤ 0
C. 5 4 < m < 4 3
D. Không tồn tại m thỏa mãn
Cho hàm số
f
(
x
)
l
n
(
e
x
+
m
)
. Có bao nhiêu số thực dương m để
f
a
+
f
b
1
với mọi số thực a,b thỏa mãn a+b1 A. 1 B. 2 C. Vô số D. 0
Đọc tiếp
Cho hàm số f ( x ) = l n ( e x + m ) . Có bao nhiêu số thực dương m để f ' a + f ' b = 1 với mọi số thực a,b thỏa mãn a+b=1
A. 1
B. 2
C. Vô số
D. 0
Cho hàm số
f
(
x
)
ln
e
x
+
m
Có bao nhiêu số thực dương m để f(a) + f(b)1 với mọi số thực a, b thỏa mãn a + b 1 A. 1 B. 2 C. Vô số D. 0
Đọc tiếp
Cho hàm số f ( x ) = ln e x + m Có bao nhiêu số thực dương m để f'(a) + f'(b)=1 với mọi số thực a, b thỏa mãn a + b = 1
A. 1
B. 2
C. Vô số
D. 0
Tìm số thực m sao cho ( m 2 -1)+(m+1)i là số ảo
![]()
![]()
![]()
![]()
Tìm tất cả các giá trị thực của tham số m sao cho phương trình
2
x
+
1
x
+
m
có nghiệm thực? A. m
≥
2 B.
m
≤
2
C.
m
≥
3
D.
m
≤
3
Đọc tiếp
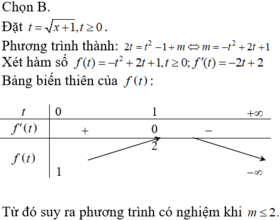
Tìm tất cả các giá trị thực của tham số m sao cho phương trình 2 x + 1 = x + m có nghiệm thực?
A. m ≥ 2
B. m ≤ 2
C. m ≥ 3
D. m ≤ 3
Cho hàm số
y
x
3
-
x
+
m
với m là một tham số thực. Số điểm cực trị của hàm số đã cho bằng A. 5 B. 4 C. 3 D. 2
Đọc tiếp
Cho hàm số y = x 3 - x + m với m là một tham số thực. Số điểm cực trị của hàm số đã cho bằng
A. 5
B. 4
C. 3
D. 2
Chọn A.

Số điểm cực trị của hàm số đã cho cũng chính là số điểm cực trj của hàm y = x 3 - x . Dựa vào tính chất của hàm số có chứa dấu giá trị tuyệt đối chúng ta dễ dàng vẽ được đồ thị của hàm y = x 3 - x như hình bên. Từ đồ thị ta nhận thấy hàm số này có 5 điểm cực trị.
Đúng 0
Bình luận (0)