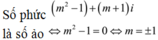Các câu hỏi tương tự
Tìm các giá trị thực của tham số m để số phức
m
3
+
3
m
2
-
4
+
(
m
-
1
)
i
là số thuần ảo. A.. B. . C. D. .
Đọc tiếp
Tìm các giá trị thực của tham số m để số phức m 3 + 3 m 2 - 4 + ( m - 1 ) i là số thuần ảo.
A.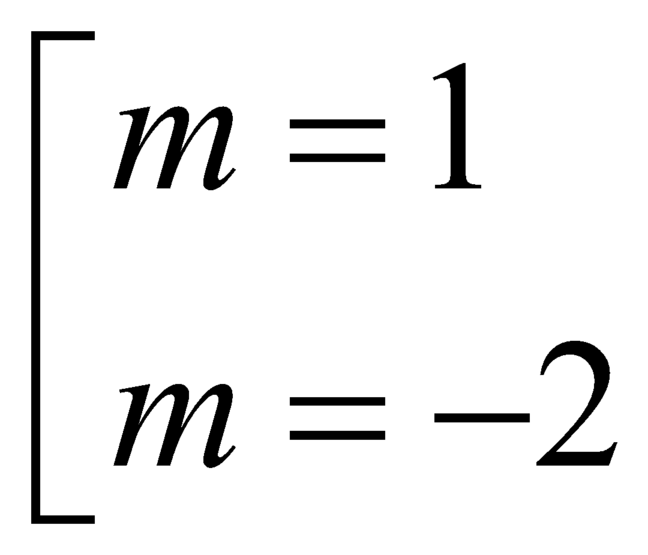 .
.
B. ![]() .
.
C. ![]()
D. ![]() .
.
Tìm giá trị của số thực m sao cho số phức
z
2
-
i
1
+
m
i
là một số thuần ảo A. Không tồn tại m. B.
m
-
1
2
C. m -2 D. m 2
Đọc tiếp
Tìm giá trị của số thực m sao cho số phức z = 2 - i 1 + m i là một số thuần ảo
A. Không tồn tại m.
B. m = - 1 2
C. m = -2
D. m = 2
Biết tập hợp điểm M biểu diễn số phức z là đường thẳng (d): 3x + 2y – 5 = 0. Tìm số phức z sao cho phần thực và phần ảo bằng nhau
A. z = 5 + 5i
B. z = 5 – 5i
C. z = -5 + 5i
D. z = 1 + i
Cho hàm số y x3- 3mx2+4m2-2 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có hai điểm cực trị A; B sao cho I( 1; 0) là trung điểm của đoạn thẳng AB. A. 0 B. -1. C. 1. D. 2.
Đọc tiếp
Cho hàm số y= x3- 3mx2+4m2-2 với m là tham số thực. Tìm giá trị của m để đồ thị hàm số có hai điểm cực trị A; B sao cho I( 1; 0) là trung điểm của đoạn thẳng AB.
A. 0
B. -1.
C. 1.
D. 2.
Gọi S là tập hợp các số thực m sao cho với mỗi
m
∈
S
có đúng một số phức thỏa mãn
z
-
m
6
và
z
z
-
4
là số thuần ảo. Tính tổng c...
Đọc tiếp
Gọi S là tập hợp các số thực m sao cho với mỗi m ∈ S có đúng một số phức thỏa mãn z - m = 6 và z z - 4 là số thuần ảo. Tính tổng của các phần tử của tập S.
A. 10
B. 0
C. 16
D. 8
Gọi S là tập hợp các số thực m sao cho với mỗi m
∈
S có đúng một số phức thỏa mãn
z
-
m
6
v
à
z
z
-
4
là số thuần ảo. Tính tổng của các phần tử của tập S
Đọc tiếp
Gọi S là tập hợp các số thực m sao cho với mỗi m ∈ S có đúng một số phức thỏa mãn z - m = 6 v à z z - 4 là số thuần ảo. Tính tổng của các phần tử của tập S
![]()
![]()
![]()
![]()
Cho điểm M là điểm biểu diễn của số phức z. Tìm phần thực và phần ảo cuả số phức z. A. Phần thực là -4 và phần ảo là 3i B. Phần thực là 3 và phần ảo là -4i C. Phần thực là -4 và phần ảo là 3 D. Phần thực là 4 và phần ảo là -4
Đọc tiếp
Cho điểm M là điểm biểu diễn của số phức z. Tìm phần thực và phần ảo cuả số phức z.
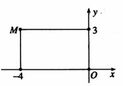
A. Phần thực là -4 và phần ảo là 3i
B. Phần thực là 3 và phần ảo là -4i
C. Phần thực là -4 và phần ảo là 3
D. Phần thực là 4 và phần ảo là -4
Cho hàm số
y
m
3
x
3
+
(
m
-
2
)
x
2
+
(
m
-
1
)
x
+
2
, với
m
là tham số thực. Tìm tất cả các giá trị thực của tham số
m
sao cho hàm số đạt cực đại tại điểm
x
1
và đạt...
Đọc tiếp
Cho hàm số y = m 3 x 3 + ( m - 2 ) x 2 + ( m - 1 ) x + 2 , với m là tham số thực. Tìm tất cả các giá trị thực của tham số m sao cho hàm số đạt cực đại tại điểm x 1 và đạt cực tiểu tại điểm x 2 thỏa mãn x 1 < x 2
A. 0 < m < 4 3
B. m ≤ 0
C. 5 4 < m < 4 3
D. Không tồn tại m thỏa mãn
Cho
I
∫
0
1
d
x
2
x
+
m
, m là số thực dương. Tìm tất cả các giá trị của m để
I
⩾
1
.
A.
0
m
⩽
1
4
B.
m
≥
1...
Đọc tiếp
Cho I = ∫ 0 1 d x 2 x + m , m là số thực dương. Tìm tất cả các giá trị của m để I ⩾ 1 .
A. 0 < m ⩽ 1 4
B. m ≥ 1 4
C. m > 0
D. 1 8 ≤ m ≤ 1 4