Các câu hỏi tương tự
Tìm giá trị của số thực m sao cho số phức
z
2
-
i
1
+
m
i
là một số thuần ảo A. Không tồn tại m. B.
m
-
1
2
C. m -2 D. m 2
Đọc tiếp
Tìm giá trị của số thực m sao cho số phức z = 2 - i 1 + m i là một số thuần ảo
A. Không tồn tại m.
B. m = - 1 2
C. m = -2
D. m = 2
Trên tập
ℂ
, cho số phức z
i
+
m
i
-
1
với m là tham số thực khác -1. Tìm tất cả các giá trị của tham số m để z.
z
¯
5 A. m -3 B. m 1 C. m
±
2 D. m
±
3
Đọc tiếp
Trên tập ℂ , cho số phức z = i + m i - 1 với m là tham số thực khác -1. Tìm tất cả các giá trị của tham số m để z. z ¯ = 5
A. m = -3
B. m = 1
C. m = ± 2
D. m = ± 3
Trên tập
ℂ
, cho số phức z
i
+
m
i
-
1
với m là tham số thực khác -1. Tìm tất cả các giá trị của tham số m để z.
z
¯
5 A. m -3 B. m 1 C. m
±
2 D. m
±
3
Đọc tiếp
Trên tập ℂ , cho số phức z = i + m i - 1 với m là tham số thực khác -1. Tìm tất cả các giá trị của tham số m để z. z ¯ = 5
A. m = -3
B. m = 1
C. m = ± 2
D. m = ± 3
Tìm tham số m để số phức z = m( m 2 -5) - mi là số thuần ảo.
A. m = 0
B. m = ± 5
C. m = 0; m = ± 5
D. m = 5
Câu 1 : Tìm tất cả các giá trị của tham số thực m để hàm số \(y=mx^3-2mx^2+\left(m-2\right)x+1\) không có cực trị
Câu 2: Tìm tất cả các giá trị thực của tham số m để hàm số \(y=\left(m-1\right)x^4-2\left(m-3\right)x^2+1\) không có cực đại
Gọi A, B là hai điểm cực trị của đồ thị hàm số f(x) = x3 - 3x2 + m với m là tham số thực khác 0. Tìm tất cả các giá trị thực của tham số m để trọng tâm tam giác OAB thuộc đường thẳng 3x + 3y - 8 = 0.
A. m = 5
B. m = 2
C. m = 6
D. m = 4
Cho số phức
z
2
+
6
i
3
-
i
m
m nguyên dương. Có bao nhiêu giá trị 1≤ m≤ 50 để z là số thuần ảo? A. 26. B. 25. C. 24. D. 50.
Đọc tiếp
Cho số phức z = 2 + 6 i 3 - i m m nguyên dương. Có bao nhiêu giá trị 1≤ m≤ 50 để z là số thuần ảo?
A. 26.
B. 25.
C. 24.
D. 50.
Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thỏa mãn z.
z
¯
1 và |z -
3
+ i|. Tìm số phần tử của S A. 1. B. 2. C. 3. D. 4
Đọc tiếp
Gọi S là tập hợp tất cả các giá trị thực của tham số m để tồn tại duy nhất số phức z thỏa mãn z. z ¯ = 1 và |z - 3 + i|. Tìm số phần tử của S
A. 1.
B. 2.
C. 3.
D. 4
Cho số phức z = 2 + 6 i 3 - i m , m nguyên dương. Có bao nhiêu giá trị m ∈ [1;50] để z là số thuần ảo?
A. 26.
B. 25.
C. 24.
D. 50.

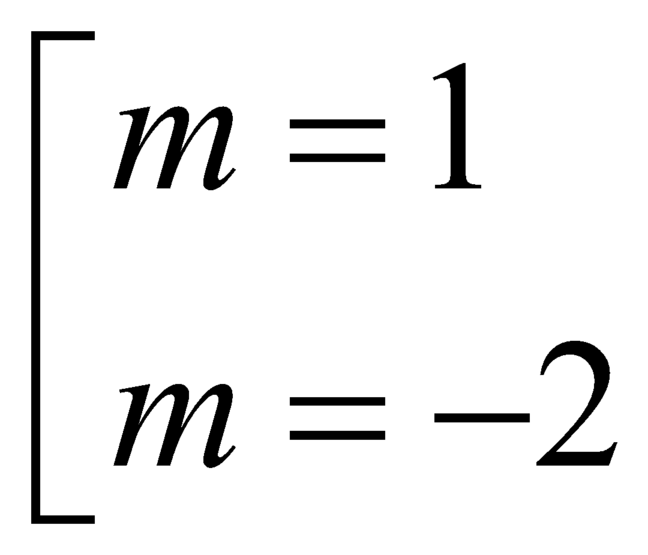 .
.