e2x _ (e+1)ex + e =0 .giải giúp em với
Những câu hỏi liên quan
Cho
F
(
x
)
(
x
-
1
)
e
x
là một nguyên hàm của hàm số
f
(
x
)
e
2
x
. Tìm nguyên hàm của hàm số
f
(
x
)
e
2
x
Đọc tiếp
Cho F ( x ) = ( x - 1 ) e x là một nguyên hàm của hàm số f ( x ) e 2 x . Tìm nguyên hàm của hàm số f ' ( x ) e 2 x
Giải giúp em ex 1 với
Phương trình
e
x
-
e
2
x
-
1
1
-
x
2
+
2
2
x
+
1
có nghiệm trong khoảng nào sau đây? A.
1
2
;
1
B.
2
;...
Đọc tiếp
Phương trình e x - e 2 x - 1 = 1 - x 2 + 2 2 x + 1 có nghiệm trong khoảng nào sau đây?
A. 1 2 ; 1
B. 2 ; 5 2
C. 1 ; 3 2
D. 3 2 ; 2
Đáp án B
Phương pháp:
Sử dụng tính đơn điệu của hàm số.
Cách giải:
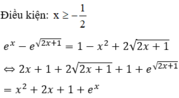
Đúng 0
Bình luận (0)
Giải phương trình sau a, 2x² +5x +3=0 b, (x-3)² =4 Giúp e với em cần gấp nha m.b
a, \(2x^2+5x+3=0\Leftrightarrow (2x+3)(x+1)=0 \Leftrightarrow\left[\begin{array}{} x=-\dfrac{3}{2}\\x=-1 \end{array} \right.\)
b, \((x-3)^2=4\Leftrightarrow (x-3)^2-2^2=0\Leftrightarrow (x-5)(x-1)=0 \Leftrightarrow\left[\begin{array}{} x=5\\x=1 \end{array} \right.\)
Đúng 1
Bình luận (0)
a: =>(x+1)(2x+3)=0
=>x=-3/2 hoặc x=-1
b: =>x-3=2 hoặc x-3=-2
=>x=1 hoặc x=5
Đúng 0
Bình luận (0)
Tính các nguyên hàm sau: ∫ e x e x + e - x d x , đặt u = e 2 x + 1
Tìm giá trị nhỏ nhất của hàm số y = e x - e - x - 2 ln ( x + 1 + x 2 ) với x ≥ 0
A. 0
B. 10
C. 2
D. -10
mọi ng giải giúp em câu e,f bài 1 với ạ
e:
\(E=\left(\dfrac{\sqrt{15}-\sqrt{20}}{2-\sqrt{3}}+\dfrac{\sqrt{21}-\sqrt{7}}{1-\sqrt{3}}\right):\dfrac{1}{\sqrt{7}-\sqrt{5}}\)
\(=\left(-\dfrac{\sqrt{5}\left(2-\sqrt{3}\right)}{2-\sqrt{3}}-\dfrac{\sqrt{7}\left(1-\sqrt{3}\right)}{1-\sqrt{3}}\right)\cdot\dfrac{\sqrt{7}-\sqrt{5}}{1}\)
\(=-\left(\sqrt{7}+\sqrt{5}\right)\left(\sqrt{7}-\sqrt{5}\right)\)
=-2
f: \(F=\sqrt{3}+1+2-\sqrt{3}=3\)
Đúng 2
Bình luận (0)
Giải giúp em ex 3 với
giúp em với ạ, giải thích cách làm giùm em luôn, e c.ơn
với a>0 và b>0, chứng minh \(\sqrt{a+b}< \sqrt{a}+\sqrt{b}\)
Ta sẽ chứng minh bằng biến đổi tương đương như sau :
Ta có : \(\sqrt{a+b}< \sqrt{a}+\sqrt{b}\left(1\right)\Leftrightarrow\left(\sqrt{a+b}\right)^2< \left(\sqrt{a}+\sqrt{b}\right)^2\Leftrightarrow a+b< a+b+2\sqrt{ab}\)
\(\Leftrightarrow2\sqrt{ab}>0\Leftrightarrow\sqrt{ab}>0\) (luôn đúng)
Vì bất đẳng thức cuối luôn đúng nên bất đẳng thức (1) được chứng minh.
Đúng 0
Bình luận (0)