i) xy - 6y + 2x - 12

= (xy - 6y) + (2x - 12)

= y(x - 6) + 2(x - 6)

= (x - 6)(y + 2)

ii) 2x(y - z) + (z - y)(x + y)

= 2x(y - z) - (y - z)(x + y)

= (y - z)(2x - x - y)

= (y - z)(x - y)

b) x + 3 = (x + 3)2 ⇔ (x + 3)2 - (x + 3) = 0 ⇔ (x + 3)(x + 3 - 1) = 0

⇔ (x + 3)(x + 2) = 0

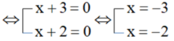
Vậy x = -3; x = -2

x² - x - y² - y

= (x - y)(x + y) - (x + y)

= (x + y)(x - y - 1)

***

9x² + y² - 16z² + 6xy

= (3x + y)² - (4z)²

= (3x + y - 4z)(3x + y + 4z)

***

a³ - a²x - ay + xy

= a²(a - x) - y(a - x)

= (a - x)(a² - y)

***

2x² - 8y² + 3x + 6y

= 2(x² - 4y²) + 3(x + 2y)

= 2(x - 2y)(x + 2y) + 3(x + 2y)

= (x + 2y)(2x - 4y + 3)

***

xy(x + y) + yz(y + z) + xz(x + z) + 2xyz

= xy(x + y + z) + yz(x + y + z) + xz(x + z)

= y(x + y + z)(x + z) + xz(x + z)

= (x + z)(xy + y² + yz + xz)

= (x + z)[y(x + y) + z(x + y)]

= (x + z)(x + y)(y + z) 

a) 2x(y-z)-6y(z-y)

=2x(y-z)+6y(y-z)

=2(y-z)(x+3y)
b)x^2+4x-4y-y^2

=x^2-y^2+4x-4y

=(x-y)(x+y)+4(x-y)

=(x-y)(x+y+4)

P/s tham khảo nha

a)  = 2x(y-z)-6y(y-z)

= 2(y-z)(x-3y)

b)  = 

1 ) \(x^2-x-y^2-y=\left(x^2-y^2\right)+\left(-x-y\right)=\left(x+y\right)\left(x-y\right)-\left(x+y\right)=\left(x+y\right)\left(x-y-1\right)\)

2 ) \(x^2-2xy+y^2-z^2=\left(x-y\right)^2-z^2=\left(x-y+z\right)\left(x-y-z\right)\)

3 ) \(5x-5y+ax-ay=5.\left(x-y\right)+a\left(x-y\right)=\left(x-y\right)\left(5+a\right)\)

4 ) \(a^3-a^2x-ay+xy=a^2.\left(a-x\right)-y.\left(a-x\right)=\left(a-x\right)\left(a^2-y\right)\)

5 ) \(xy.\left(x+y\right)+yz.\left(y+z\right)+xz.\left(x+z\right)+2xyz\)

\(=xy.\left(x+y\right)+y^2z+yz^2+x^2z+xz^2+xyz+xyz\)

\(=xy.\left(x+y\right)+\left(y^2z+xyz\right)+\left(yz^2+xz^2\right)+\left(x^2z+xyz\right)\)

\(=xy.\left(x+y\right)+yz.\left(x+y\right)+z^2.\left(x+y\right)+xz.\left(x+y\right)\)

\(=\left(x+y\right)\left(xy+yz+z^2+xz\right)=\left(x+y\right)\left[\left(xy+xz\right)+\left(yz+z^2\right)\right]\)

\(=\left(x+y\right)\left[x.\left(y+z\right)+z.\left(y+z\right)\right]=\left(x+y\right)\left(y+z\right)\left(x+z\right)\)

A ) xy(z+y)+yz(y+z)+zx(z+x)

=y.[x(z+y)+z(y+z)]+zx(z+x)

=y.(xz+xy+zy+z²)+zx(z+x)

=y.(xz+z²+xy+zy)+zx(z+x)

=y.[z.(z+x)+y.(z+x)]+zx(z+x)

=y.(z+x)(z+y)+zx(z+x)

=(z+x)[y(z+y)+zx]

=(z+x)(yz+y²+zx)

B )xy(x+y)-yz(y+z)-zx(z-x)

=y.[x(x+y)-z(y+z)]-zx(z-x)

=y.(x²+xy-zy-z²)-zx(z-x)

=y.(x²-z²+xy-zy)-zx(z-x)

=y.[(x+z)(x-z)+y.(x-z)]-zx(z-x)

=y.(x-z)(x+z+y)+zx(x-z)

=(x-z)[y(x+z+y)+zx]

=(x-z)(yx+yz+y²+zx)

=(x-z)(yx+zx+yz+y²)

=(x-z)[x.(y+z)+y.(y+z)]

=(x-z)(y+z)(x+y)

b. \(\text{ xy(x+y)-yz(y+z)-xz(z-x) =xy(x+y+z-z)+yz(y+z)+xz(x-z) =xy(x-z)+xy(y+z)+yz(y+z)+xz(x-z) =(x+y)(y+z)(x-z) }\)

\(xy\left(x-y\right)-xz\left(x+z\right)+yz\left(2x-y+z\right)\)

\(=xy\left(x-y\right)-xz\left(x+z\right)+yz\left(x-y+x+z\right)\)

\(=xy\left(x-y\right)-xz\left(x+z\right)+yz\left(x-y\right)+yz\left(x+z\right)\)

\(=\left(x-y\right)\left(xy+yz\right)-\left(xz-yz\right)\left(x+z\right)\)

\(=y\left(x-y\right)\left(x+z\right)-z\left(x-y\right)\left(x+z\right)\)

\(=\left(y-z\right)\left(x-y\right)\left(x+z\right)\)

Ta có :

xy(x−y)−xz(x+z)+yz(2x−y+z)

=xy(x−y)−xz(x+z)+yz(x−y+x+z)

=xy(x−y)−xz(x+z)+yz(x−y)+yz(x+z)

=(x−y)(xy+yz)−(xz−yz)(x+z)

=y(x−y)(x+z)−z(x−y)(x+z)

=(y−z)(x−y)(x+z)

P/s tham khảo nha

xy(x + y) + yz(y + z) + xz(x + z) + 2xyz

= x 2 y + x y 2  + yz(y + z) +  x 2 z + x z 2  + xyz + xyz

= ( x 2 y +  x 2 z) + yz(y + z) + (x y 2  + xyz) + (x z 2  + xyz)

=  x 2 (y + z) + yz(y + z) + xy(y+ z) + xz(y + z)

= (y + z)(  x 2  + yz + xy + xz) = (y + z)[( x 2  + xy) + (xz + yz)]

= (y + z)[x(x + y) + z(x + y)] = (y + z)(x+ y)(x + z)

x³ - 3x²y + 3xy² - y³ - z³

= (x³ - 3x²y + 3xy² - y³) - z³

= (x - y)³ - z³

= (x - y - z)[(x - y)² + (x - y)z + z²]

= (x - y - z)(x² - 2xy + y² + xz - yz + z³)

--------------------

x² - y² + 8x + 6y + 7

= (x² + 8x + 16) - (y² - 6y + 9)

= (x + 4)² - (y - 3)²

= (x + 4 - y + 3)(x + 4 + y - 3)

= (x - y + 7)(x + y + 1)

a: \(=\left(x^3-3x^2y+3xy^2-y^3\right)-z^3\)

\(=\left(x-y\right)^3-z^3\)

\(=\left(x-y-z\right)\left[\left(x-y\right)^2+z\left(x-y\right)+z^2\right]\)

\(=\left(x-y-z\right)\left(x^2-2xy+y^2+xz-yz+z^2\right)\)

b: \(=x^2+8x+16-y^2+6y-9\)

=(x+4)^2-(y-3)^2

=(x+4+y-3)(x+4-y+3)

=(x+y+1)(x-y+7)