Hình thang cân ABCD (AB//CD) có AB=4cm, CD=14cm, BC=13cm. Tính độ dài BD.

Những câu hỏi liên quan
1/ cho hình thang cân ABCD ( AB // CD ), AB = 4cm, CD = 14cm, BC = 13cm. Tính BD.
2/ Cho hình thang cân ABCD (AB// CD ) AB = 9cm, CD = 15cm, AC vuông góc với BD. Tính đường cao BH.
Hình thang cân ABCD(AB//CD) có AB=4cm, CD=14cm, BC=13cm
Tính độ dài BD?
Cho hình thang ABCD, AB song song CD, góc A bằng 90 độ, AB<CD. Biết BC=13cm; CD=14cm; BD=15cm. Tính AB
1/ cho hình thang cân ABCD ( AB // CD ), AB = 4cm, CD = 14cm, BC = 13cm. Tính BD.
Bài 1 : Cho hình thang cân ABCD ( AB// CD), vẽ đường cao BH. Biết AB=4cm, CD=14cm. Tính BD?
Bài 2: Cho hình thang ABCD có M là trung điểm BC biết DM là phân giác góc D. CMR: góc AMD=90 độ
Tính diện tích hình thang ABCD trong các trường hợp sau:1, Góc A Góc B90°; góc ADC45°; AB4cm; AD12cm2, ABCD là hình thang cân( AB// CD và ABCD);AH 8cm; HC12cm( với H là hình chiếu vuông góc của A trên CD)3, AB // CD, góc C30°, AB3cm, BC8cm; CD12 cm4, ABCD là hình thang cân có các cạnh đáy với độ dài lần lượt là 10cm, 20cm, và độ dài cạnh bên 13cm5, ABCD là hình thang cân( AB//CD) có AB 13cm, CD23cm và CA là tia phân giác góc BCDMỌI NGƯỜI LÀM ƠN GIÚP MÌNH VỚI !!!
Đọc tiếp
Tính diện tích hình thang ABCD trong các trường hợp sau:
1, Góc A= Góc B=90°; góc ADC=45°; AB=4cm; AD=12cm
2, ABCD là hình thang cân( AB// CD và AB<CD);AH =8cm; HC=12cm( với H là hình chiếu vuông góc của A trên CD)
3, AB // CD, góc C=30°, AB=3cm, BC=8cm; CD=12 cm
4, ABCD là hình thang cân có các cạnh đáy với độ dài lần lượt là 10cm, 20cm, và độ dài cạnh bên =13cm
5, ABCD là hình thang cân( AB//CD) có AB =13cm, CD=23cm và CA là tia phân giác góc BCD
MỌI NGƯỜI LÀM ƠN GIÚP MÌNH VỚI !!!
Cho hình thang vuông ABCD có ∠ A = ∠ D = 90 ° , AB = 4cm, BC = 13cm, CD = 9cm. Tính độ dài AD
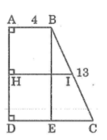
Kẻ BE ⊥ CD
Suy ra tứ giác ABED là hình chữ nhật
Ta có: AD = BE
AB = DE = 4 (cm)
Suy ra: CE = CD – DE = 9 – 4 = 5 (cm)
Áp dụng định lí Pitago vào tam giác vuông BCE ta có :
B C 2 = B E 2 + C E 2
Suy ra : B E 2 = B C 2 - C E 2 = 13 2 - 5 2 = 144
BE = 12 (cm)
Vậy: AD = 12 (cm)
Đúng 0
Bình luận (0)
Cho hình vuông ABCD vuông tại A có AB//CD và AB<CD. Kẻ AH vuông góc với BD tại H. Tính BH và diện tích hình thang ABCD nếu biết BC=13cm, CD=14cm và DB=15cm
Bài 1. Cho hình thang cân ABCD (AB\\CD) có AB=8cm, BC=AD=5cm, CD=14cm. Kẻ các đường cao AK và BH.
a) Chứng minh rằng CH=DK.
b) Chứng minh: CD-AB=2AK. Từ đó tính độ dài BH.
c) Tính diện tích hình thang ABCD.
Bài 2. Hình thang cân ABCD có đáy nhỏ AB bằng cạnh bên BC. Chứng minh CA là tia phân giác của góc BCD.
Bài 2:
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{ACD}\)
nên \(\widehat{ACB}=\widehat{ACD}\)
hay CA là tia phân giác của \(\widehat{BCD}\)
Đúng 2
Bình luận (0)













