\(a,P=5x\left(2-x\right)-\left(x+1\right)\left(x+9\right)\)

\(=10x-5x^2-\left(x^2+x+9x+9\right)\)

\(=10x-5x^2-x^2-x-9x-9\)

\(=\left(10x-x-9x\right)+\left(-5x^2-x^2\right)-9\)

\(=-6x^2-9\)

Ta thấy: \(x^2\ge0\forall x\)

\(\Rightarrow-6x^2\le0\forall x\)

\(\Rightarrow-6x^2-9\le-9< 0\forall x\)

hay \(P\) luôn nhận giá trị âm với mọi giá trị của biến \(x\).

\(b,Q=3x^2+x\left(x-4y\right)-2x\left(6-2y\right)+12x+1\)

\(=3x^2+x^2-4xy-12x+4xy+12x+1\)

\(=\left(3x^2+x^2\right)+\left(-4xy+4xy\right)+\left(-12x+12x\right)+1\)

\(=4x^2+1\)

Ta thấy: \(x^2\ge0\forall x\)

\(\Rightarrow4x^2\ge0\forall x\)

\(\Rightarrow4x^2+1\ge1>0\forall x\)

hay \(Q\) luôn nhận giá trị dương với mọi giá trị của biến \(x\) và \(y\).

#\(Toru\)

Điều kiện x  ≠  0 và x  ≠  -3

Ta có:

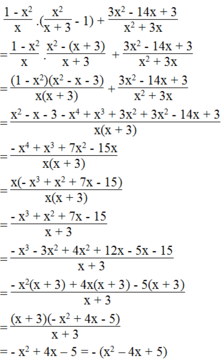
Vì x 2 - 4 x + 5 = x 2 - 4 x + 4 + 1 = x - 2 2 + 1 > 0 với mọi giá trị của x nên

- x 2 + 4 x - 5 = - x - 2 2 + 1 < 0 với mọi giá trị của x.

Vậy giá trị biểu thức luôn luôn âm với mọi giá trị x  ≠  0 và x ≠ -3

a) \(A=x^2+2x+3=x^2+2x+1+2\)

\(=\left(x+1\right)^2+2\ge2\)

Vậy A luôn dương với mọi x

b) \(B=-x^2+4x-5=-\left(x^2-4x+5\right)\)

\(=-\left(x^2-4x+2^2\right)-1\)

\(=-\left(x-2\right)^2-1\le-1\)

Vậy B luôn âm với mọi x

a)\(x^2+2x+3=\left(x^2+2x+1\right)+2=\left(x+1\right)^2+2\ge2\)

Vậy x² +2x+3 luôn dương.

b)\(-x^2+4x-5=-\left(x^2-4x+5\right)=-\left(x^2-4x+4+1\right)=-\left[\left(x-2\right)^2+1\right]\le-1\)

Vậy -x² +4x-5 luôn luôn âm.

a.x²+ 2x+ 3

=x²+ 2.x.1+ 1²- 1²+ 3

= (x+1)² -1+3

= (x+1)²+ 2

Ta có: (x+1)² ≥0

           (x+1)²+ 3≥ 3>0

⇒x²+ 2x+ 3>0 mọi x

Vậy x²+ 2x+3>0 mọi x

b. -x²+ 4x- 5

= - (x²- 4x +5)

= - (x²- 2.x.2+ 2²- 2²+ 5)

= - ((x- 2)²- 4+ 5)

= - ((x- 2)²+1)

= -(x- 2)² -1

Ta có: (x-2)² ≥0

         - (x-2)² ≤0

         - (x-2)² +1≤ 1

⇒ -x²+ 4x- 5 <0 mọi x

Vậy -x²+ 4x- 5 <0 mọi x

a) \(x^2+x+1=x^2+x+\frac{1}{4}+\frac{3}{4}=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}>0\forall x\)

c) \(C=4x-10-x^2=-\left(x^2-4x+10\right)\)

\(=-\left(x^2-4x+4+6\right)=-\left[\left(x-2\right)^2+6\right]\)

\(=-\left(x^2-4x+4+6\right)=-\left[\left(x-2\right)^2\right]-6\le-6< 0\forall x\)

Bài 1

\(a,\)\(49x^2-28x+7\)

\(=\left(7x\right)^2-2.7x.2+2^2+3\)

\(=\left(7x-2\right)^2+3\ge3\)( luôn dương )

Dấu bằng sảy ra khi và chỉ khi \(\left(7x-2\right)^2=0\)

\(\Rightarrow7x-2=0\)

\(\Rightarrow x=\frac{2}{7}\)

Bài 1 b

\(x^2+\frac{2}{5}x+\frac{1}{5}\)

\(=x^2+2.x.\frac{1}{5}+\frac{1}{25}+\frac{4}{25}\)

\(=\left(x+\frac{1}{5}\right)^2+\frac{4}{25}\ge\frac{4}{25}\)( luôn dương )

Dấu bằng sảy ra khi và chỉ khi \(\left(x+\frac{1}{5}\right)^2=0\)

\(\Rightarrow x+\frac{1}{5}=0\)

\(\Rightarrow x=-\frac{1}{5}\)

Bài 2 a

\(-9x^2+24x-12\)

\(=-\left(3x^2-2.3x.4+4^2-4\right)\)

\(-\left[\left(3x-4\right)^2-4\right]\)

\(=-\left(3x-4\right)^2+4\)

Sai đề chăng ?

\(E=3y^2+y+10\)

\(=3\left(y^2+\frac{1}{3}y+\frac{1}{36}\right)+9\frac{11}{12}\)

\(=3\left(y+\frac{1}{6}\right)^2+9\frac{11}{12}>0\)

Vậy E luôn dương với mọi y

\(4x^2-8x+5=\left(2x\right)^2-2.2.2x+4+1=\left(2x-1\right)^2+1>0\)(luon duong)

\(4x^2-8x+5\)

\(=\left(2x\right)^2-2×2×2x+1+4\)

\(=\left(2x-1\right)^2+1\)

\(\Rightarrow\left(2x-1\right)^2+1>0\)

Vậy biểu thức trên luôn dương !!!

Không biê