Tam giác có 4 điểm sau đây trùng nhau: trọng tâm; trực tâm; điểm cách đều 3 cạnh, điểm cách đều 3 đỉnh là tam giác nào:
A.Tam giác cân B.Tam giác đều C.Tam giác vuông D.Tam giác nhọn
Trong mỗi câu dưới đây, hãy chọn phương án trả lời đúng:
Tam giác nào sau đây có trọng tâm, trực tâm trùng nhau.
A. Tam giác cân
B. Tam giác đều
C. Tam giác vuông
D. Tam giác tù
Tam giác nào trong các tam giác dưới đây có trọng tâm, trực tâm trùng nhau.
A. Tam giác vuông
B. Tam giác cân
C. Tam giác đều
D. Tam giác tù
Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Chứng minh rằng:
a) Nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau;
b) Nếu tam giác ABC có hai điểm trong bốn điểm G, H, I, O trùng nhau thì tam giác ABC là tam giác đều.
a)
Ta có:
G là trọng tâm của tam giác ABC (giao điểm của ba đường trung tuyến);
H là trực tâm của tam giác ABC (giao điểm của ba đường cao);
I là giao điểm của ba đường phân giác của tam giác ABC;
O là giao điểm của ba đường trung trực của tam giác ABC (Đường trung trực đi qua trung điểm của cạnh và vuông góc với cạnh tại trung điểm đó).
Mà tam giác ABC đều nên trong tam giác ABC đường trung tuyến đồng thời là đường cao và là đường phân giác.
Vậy bốn điểm G, H, I, O trùng nhau hay nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau.
b)
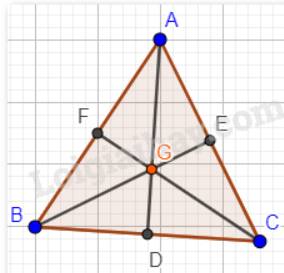
Giả sử trong tam giác ABC có hai điểm trùng nhau là H (trực tâm của tam giác) và I (giao của ba đường phân giác).
Hay AD, BE, CF vừa là đường cao, vừa là đường phân giác của tam giác ABC.
Xét tam giác ADB và tam giác ADC có:
\(\widehat {BAD} = \widehat {CAD}\) ( vì AD là tia phân giác của góc BAC)
AD chung;
\(\widehat {ADB} = \widehat {ADC}(=90^0)\) (vì \(AD \bot BC\));
Vậy \(\Delta ADB = \Delta ADC\)(g.c.g). Suy ra: AB = AC( 2 cạnh tương ứng). (1)
Tương tự ta có: \(\Delta AEB = \Delta CEB\)(c.g.c). Suy ra: AB = BC ( 2 cạnh tương ứng). (2)
Từ (1) và (2) suy ra: AB = BC = AC.
Vậy tam giác ABC đều hay nếu tam giác ABC có hai điểm trong bốn điểm G, H, I, O trùng nhau thì tam giác ABC là tam giác đều.
Cho tam giác ABC, H là trực tâm, O la tâm đường tròn ngoại tiếp.M là trung điểm BC,N là trung điểm AH.CMR: Trọng tâm tam giác ABC và OMN trùng nhau
Gọi G là trọng tâm của \(\Delta\)ABC. Từ A kẻ đường kính AK của (O), nối K vs B &C
2 đoạn AM và ON gặp nhau ở điểm I.
Xét đường tròn (O) có đường kính AK, 2 điểm B & C cùng thuộc đường tròn (O)
=> AB vuông BK và AC vuông CK. Mà CH vuông A; BH vuông AC
=> BH//CK; CH//BK (Quan hệ //, vuông góc) => Tứ giác BHCK là hình bình hành.
Ta có M là trung điểm đường chéo BC của hbh BHCK => M là trung điểm HK
Xét \(\Delta\)AKH: O là trung điểm AK; M là trung điểm HK => OM là đường trung bình \(\Delta\)AKH
=> OM//AH và OM=1/2.AH. Lại có: AN=NH=1/2.AH => OM//AN và OM=AN
=> Tứ giác AOMN là hbh. Do I là giao điểm 2 đg chéo nên I là trung điểm ON và AM
=> MI là trung tuyến \(\Delta\)OMN
Ta thấy: G là trọng tâm \(\Delta\)ABC => MG=1/3.AM. Mà AM=2.MI
=> MG=1/3.2.MI=2/3.MI. Xét \(\Delta\)OMN có: Trung tuyến MI, điểm G thuộc MI
Và MG=2/3.MI (cmt) => G là trọng tâm của \(\Delta\)OMN. Mà G cũng là trọng tâm \(\Delta\)ABC
=> 2 tam giác ABC và OMN có chung 1 trọng tâm G (đpcm).
chứng minh rằng trong tam giác đều trọng tâm và giao điểm của 2 đường phân giác trong tam giác trùng nhau
Các điểm A'(-4; 1), B'(2; 4), C'(2; -2) lần lượt là trung điểm các cạnh BC, CA và AB của tam giác ABC. Tính tọa độ các đỉnh của tam giác ABC. Chứng minh rằng trọng tâm của tam giác ABC và A'B'C' trùng nhau.
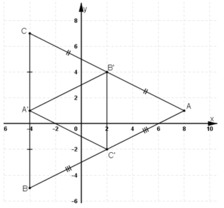
A’ là trung điểm của BC 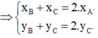
B’ là trung điểm của AC 
C’ là trung điểm của BA 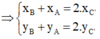
Gọi G là trọng tâm ΔABC và G’ là trọng tâm ΔA’B’C’
Ta có :
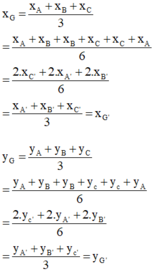
Vậy G ≡ G’ (đpcm)
vẽ hình đối xứng của tam giác abc qua điểm o cho trước trong các trường hợp sau a) o trùng với trọng tâm g của tam giác b) o trùng với đỉnh a của tam giác
Cho tam giác ABC. Gọi G là trọng tâm tam giác. H là trực tâm tam giác. I là giao điểm 3 đường phân giác. O là điểm cách đều 3 đỉnh tam giác.
Chứng minh rằng: tam giác ABC là tam giác đều khi và chỉ khi các điểm G,H,I,O trùng nhau và ngược lại.
Thiên Ngoại Phi Tiên sai rồi cậu lấy trêm mạn mà đúng gì nẫu nói G là trực tâm H là đường cao , o cách đều ba đỉnh mà sao không có ba diểm đó
Trong mặt phẳng toạ độ Oxy, cho tam giác ABC có trung điểm các cạnh BC, CA, AB tương ứng là M(2 ; 0), N4 ; 2), P(1 ; 3).
a) Tìm toạ độ các điểm A, B, C.
b) Trọng tâm hai tam giác ABC và MNP có trùng nhau không? Vì sao?
a) Do M, N, P là trung điểm của các cạnh BC, CA, AB nên:
\(\left\{ \begin{array}{l}\frac{{{x_B} + {x_C}}}{2} = {x_M}\\\frac{{{x_B} + {x_A}}}{2} = {x_P}\\\frac{{{x_A} + {x_C}}}{2} = {x_N}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_B} + {x_C} = 4\\{x_B} + {x_A} = 2\\{x_A} + {x_C} = 8\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{x_A} = 3\\{x_B} = - 1\\{x_C} = 5\end{array} \right.\) và \(\left\{ \begin{array}{l}\frac{{{y_B} + {y_C}}}{2} = {y_M}\\\frac{{{y_B} + {y_A}}}{2} = {y_P}\\\frac{{{y_A} + {y_C}}}{2} = {y_N}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_B} + {y_C} = 0\\{y_B} + {y_A} = 4\\{y_A} + {y_C} = 6\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}{y_A} = 5\\{y_B} = - 1\\{y_C} = 1\end{array} \right.\)
Vậy \(A\left( {3;5} \right),B\left( { - 1; - 1} \right),C\left( {5;1} \right)\)
b) Trọng tâm tam giác ABC có tọa độ là: \(\left\{ \begin{array}{l}\frac{{{x_A} + {x_B} + {x_C}}}{3} = \frac{{3 + \left( { - 1} \right) + 5}}{3} = \frac{7}{3}\\\frac{{{y_A} + {y_B} + {y_C}}}{3} = \frac{{5 + \left( { - 1} \right) + 1}}{3} = \frac{5}{3}\end{array} \right.\)
Trọng tâm tam giác MNP có tọa độ là: \(\left\{ \begin{array}{l}\frac{{{x_M} + {x_N} + {x_P}}}{3} = \frac{{2 + 4 + 1}}{3} = \frac{7}{3}\\\frac{{{y_M} + {y_N} + {y_P}}}{3} = \frac{{0 + 2 + 3}}{3} = \frac{5}{3}\end{array} \right.\)
Vậy trọng tâm của 2 tam giác ABC và MNP là trùng nhau vì có cùng tọa độ.