Cho hình chóp S.ABC. Lấy M∈SC, N∈BC, P∈SA, Q∈AB. Tìm giao tuyến của hai mặt phẳng (AMN) và mp(CPQ)

Những câu hỏi liên quan
Cho hình chóp đỉnh S có đáy là hình thang ABCD với AB là đáy lớn. Gọi M, N theo thứ tự là trung điểm của các cạnh SB và SC.
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC)
b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN)
c) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN)
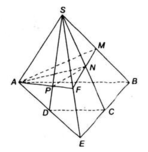
a) Tìm (SAD) ∩ (SBC)
Gọi E= AD ∩ BC. Ta có:
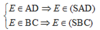
Do đó E ∈ (SAD) ∩ (SBC).
mà S ∈ (SAD) ∩ (SBC).
⇒ SE = (SAD) ∩ (SBC)
b) Tìm SD ∩ (AMN)
+ Tìm giao tuyến của (SAD) và (AMN) :
Trong mp (SBE), gọi F = MN ∩ SE :
F ∈ SE ⊂ (SAD) ⇒ F ∈ (SAD)
F ∈ MN ⊂ (AMN) ⇒ F ∈ (AMN)
⇒ F ∈ (SAD) ∩ (AMN)
⇒ AF = (SAD) ∩ (AMN).
+ Trong mp (SAD), gọi AF ∩ SD = P
⇒ P = SD ∩ (AMN).
c) Tìm thiết diện với mp(AMN):
(AMN) ∩ (SAB) = AM;
(AMN) ∩ (SBC) = MN;
(AMN) ∩ (SCD) = NP
(AMN) ∩ (SAD) = PA.
⇒ Thiết diện cần tìm là tứ giác AMNP.
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có
S
A
⊥
(
A
B
C
)
v
à
S
A
2
B
C
,
B
A
C
^
120
°
. Hình chiếu của A trên đoạn SB, SC lần lượt là M, N. Tính góc giữa hai mặt phẳng (ABC) và (AMN). A. 30
°
B. 45...
Đọc tiếp
Cho hình chóp S.ABC có S A ⊥ ( A B C ) v à S A = 2 B C , B A C ^ = 120 ° . Hình chiếu của A trên đoạn SB, SC lần lượt là M, N. Tính góc giữa hai mặt phẳng (ABC) và (AMN).
A. 30 °
B. 45 °
C. 60 °
D. 90 °
Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của SA và BC. P là điểm nằm trên cạnh AB sao cho
A
P
A
B
1
3
. Gọi Q là giao điểm của SC với mặt phẳng
M
N
P
. Tính
S
Q
S
C...
Đọc tiếp
Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của SA và BC. P là điểm nằm trên cạnh AB sao cho A P A B = 1 3 . Gọi Q là giao điểm của SC với mặt phẳng M N P . Tính S Q S C
A. 1 3
B. 1 6
C. 1 2
D. 2 3
Chọn A.
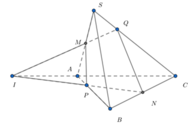
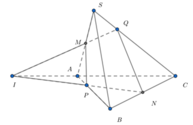
Phương pháp : Dựng điểm Q và áp dụng định lý Menenaus.
Cách giải : Gọi I là giao điểm của PN và AC. Suy ra Q là giao điểm của IM và SC.
Áp dụng định lý Menenaus cho tam giác SAC ta có :
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của SA và BC. P là điểm nằm trên cạnh AB sao cho
A
P
A
B
1
3
. Gọi Q là giao điểm của SC với mặt phẳng (MNP). Tính
S
Q
S
C
Đọc tiếp
Cho hình chóp S.ABC. Gọi M, N lần lượt là trung điểm của SA và BC. P là điểm nằm trên cạnh AB sao cho A P A B = 1 3 . Gọi Q là giao điểm của SC với mặt phẳng (MNP). Tính S Q S C
![]()
![]()
![]()
Chọn đáp án A
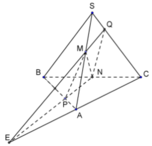
Trong mặt phẳng (ABC), gọi E = NP ∩ AC
Khi đó Q chính là giao điểm của SC với EM
Áp dụng định lý Menelaus vào tam giác ABC ta có:
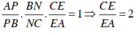
Áp dụng định lý Menelaus vào tam giác SAC ta có:
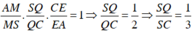
Đúng 0
Bình luận (0)
Cho hình chóp đỉnh S có đáy là hình thang ABCD với AB là đáy lớn. Gọi M, N theo thứ tự là trung điểm của các cạnh SB và SC
a) Tìm giao tuyến của hai mặt phẳng (SAD) và (SBC) ?
b) Tìm giao điểm của đường thẳng SD với mặt phẳng (AMN) ?
c) Tìm thiết diện của hình chóp S.ABCD cắt bởi mặt phẳng (AMN) ?
a) (SAD) ∩ (SBC) = SE
b) Trong (SBE): MN ∩ SE = F
Trong (SAE): AF ∩ SD = P là điểm cần tìm
c) Thiết diện là tứ giác AMNP
Đúng 0
Bình luận (0)
Cho hình chóp S.ABC có SA
⊥
(ABC), SA2SB và góc BAC
120
O
. Hình chiếu của A trên các đoạn SB, SC lần lượt là M, N. Tính góc giữa hai mặt phẳng (ABC) và (AMN) A.
45
o
B.
60
o
C.
15
o
D.
30
o
Đọc tiếp
Cho hình chóp S.ABC có SA ⊥ (ABC), SA=2SB và góc BAC = 120 O . Hình chiếu của A trên các đoạn SB, SC lần lượt là M, N. Tính góc giữa hai mặt phẳng (ABC) và (AMN)
A. 45 o
B. 60 o
C. 15 o
D. 30 o
Cho hình Chóp S.ABCD có đáy là hình thang, đáy lớn AB. Gọi O là giao điểm của AC và BD
a. Tìm giao tuyến của hai mặt phẳng (SAD) và (SAB), (SAB)và (SCD)
b. Trên SC lấy điểm M tùy ý. Tìm giao điểm K của SD và mp (ABM)
c. Tìm thiết diện của hình chóp với mặt phẳng (ABM)
giúp mình với
Cho hình chóp S.ABC có SASBCACBABa,
S
C
a
3
2
, G là trọng tâm của tam giác ABC. là mặt phẳng đi qua G, song song với các đường thẳng AB và SB. Gọi M, N, P lần lượt là giao điểm của với các đường thẳng BC, AC, SC. Góc giữa hai mặt phẳng (MNP) và (ABC) bằng A. ...
Đọc tiếp
Cho hình chóp S.ABC có SA=SB=CA=CB=AB=a, S C = a 3 2 , G là trọng tâm của tam giác ABC. là mặt phẳng đi qua G, song song với các đường thẳng AB và SB. Gọi M, N, P lần lượt là giao điểm của với các đường thẳng BC, AC, SC. Góc giữa hai mặt phẳng (MNP) và (ABC) bằng
A. 90 0 C
B. 45 0 C
C. 30 0 C
D. 60 0 C
Chọn đáp án D
Ta có
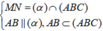
![]()
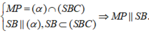
![]()
Khi đó ![]()
Gọi I là trung điểm của AB.
Ta có SA=SB=AB=CA=CB=a nên tam giác SAB và tam giác ABC đều cạnh a.
Khi đó A B ⊥ S I , A B ⊥ C I và S I = C I = a 3 a
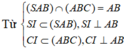
![]()
Mặt khác S I = C I = S C = a 3 2 nên ∆ S I C đều
![]()
Vậy góc giữa hai mặt phẳng (MNP) và (ABC) bằng 60 0
Đúng 0
Bình luận (0)
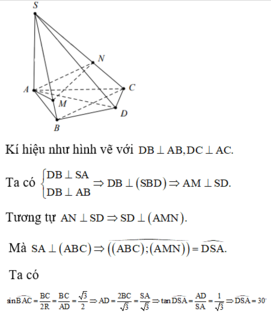
Cho hình chóp S.ABC có SA vuông góc với đáy,
S
A
2
B
C
v
à
B
A
C
^
120
°
. Hình chiếu của A trên các đoạn SB, SC lần lượt là M, N. Tính góc giữa hai mặt phẳng (ABC) và (AMN) A.
45
°
B.
60
°
C.
15
°
D. ...
Đọc tiếp
Cho hình chóp S.ABC có SA vuông góc với đáy, S A = 2 B C v à B A C ^ = 120 ° . Hình chiếu của A trên các đoạn SB, SC lần lượt là M, N. Tính góc giữa hai mặt phẳng (ABC) và (AMN)
A. 45 °
B. 60 °
C. 15 °
D. 30 °
Đáp án D
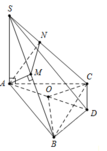
Gọi O là tâm đường tròn ngoại tiếp tam giác ABC.
Và D là điểm đối xứng với A qua O.

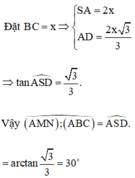
Đúng 0
Bình luận (0)