Chọn A.
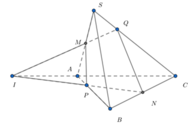
Phương pháp : Dựng điểm Q và áp dụng định lý Menenaus.
Cách giải : Gọi I là giao điểm của PN và AC. Suy ra Q là giao điểm của IM và SC.
Áp dụng định lý Menenaus cho tam giác SAC ta có :
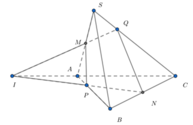
Chọn A.

Phương pháp : Dựng điểm Q và áp dụng định lý Menenaus.
Cách giải : Gọi I là giao điểm của PN và AC. Suy ra Q là giao điểm của IM và SC.
Áp dụng định lý Menenaus cho tam giác SAC ta có :

Cho hình chóp S.ABC có mỗi mặt bên là một tam giác vuông và S A = S B = S C = a . Gọi M, N, P lần lượt là trung điểm của các cạnh AB, AC, BC; D là điểm đối xứng của S qua P. I là giao điểm của đường thẳng AD với mặt phẳng (SMN). Tính theo a thể tích của khối tứ diện MBSI.
A. a 3 12 .
B. a 3 36 .
C. a 3 6 .
D. 2 a 3 12 .
Cho hình chóp S.ABC có S A = S B = S C = 3 , tam giác ABC vuông cân tại B và
A C = 2 2 . Gọi M, N lần lượt là trung điểm của AC và BC. Trên hai cạnh SA, SB lấy các điểm P, Q tương ứng sao cho S P = 1 , S Q = 2. Tính thể tích V của khối tứ diện M N P Q .
A. V = 7 18
B. V = 3 12
C. V = 34 12
D. V = 34 144
Cho hình chóp S.ABC có SA ^ (ABC), AB = 1, AC = 2 và B A C ⏜ = 60 ° . Gọi M , N lần lượt là hình chiếu của A trên SB, SC. Tính bán kính R của mặt cầu đi qua các điểm A, B, C, M, N
A. R = 2
B. R = 2 3 3
C. R = 4 3
D. R = 1
Cho hình chóp S.ABC có S A ⊥ ( A B C ) , A B = 1 , A C = 2 , B A C ^ = 60 ° Gọi M, N lần lượt là hình chiếu của A trên SB, SC. Tính bán kính R của mặt cầu đi qua các điểm A,B,C,M,N
![]()
![]()
![]()
![]()
Cho hình chóp S.ABC có A S B ^ = B S C ^ = C S A ^ = 90 ° , S A = 1 , S B = 2 , S C = x , x > 0 . Gọi M, N, P lần lượt là trung điểm của các cạnh AB, BC, CA. Biết rằng hai mặt phẳng (SMN) và (SMP) vuông góc với nhau. Giá trị của x bằng
A. 2 5 2
B. 2
C. 5 2
D. 5
Cho hình chóp S.ABCD có đáy hình thoi cạnh 3a, SA=SD=3a, SB=SC=3a 3 . Gọi M, N lần lượt là trung điểm của các cạnh SA và SD, P là điểm thuộc cạnh AB sao cho AP=2a Tính diện tích thiết diện của hình chóp khi cắt bởi mặt phẳng (MNP)
![]()
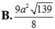
![]()
![]()
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, hai mặt phẳng (SAB) và (SAD) cùng vuông góc với đáy, biết S C = 3 Gọi M, N, P, Q lần lượt là trung điểm của SB, SD, CD, BC. Tính thể tích của khối chóp A.MNPQ
A . a 3 3
B . a 3 8
C . a 3 12
D . a 3 4
Cho hình chóp S.ABC có SA=SB=CA=CB=AB=a, S C = a 3 2 , G là trọng tâm của tam giác ABC. là mặt phẳng đi qua G, song song với các đường thẳng AB và SB. Gọi M, N, P lần lượt là giao điểm của với các đường thẳng BC, AC, SC. Góc giữa hai mặt phẳng (MNP) và (ABC) bằng
A. 90 0 C
B. 45 0 C
C. 30 0 C
D. 60 0 C
Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh a, SA vuông góc với mặt đáy. Gọi M là trung điểm của BC. Mặt phẳng (P) đi qua A và vuông góc với SM cắt SB, SC lần lượt tại E, F. Biết V S . A E F = V S . A B C . Tính thể tích V của khối chóp S.ABC.
A. a 3 2
B. a 3 8
C. 2 a 3 5
D. a 3 12