Cho hàm số y = ( m^2 + m + 1 )x - 2
Chứng minh rằng : Hàm số này luôn đồng biến
#Giúp tớ nhes ....đang cần gấp
Những câu hỏi liên quan
Cho hàm số y=(m4+2m2+12m+10)x+m-1.chứng minh rằng hàm số luôn đồng biến R
Cho hàm số y=(2m2-4m+7)x+3m2-m-1.Chứng minh hàm số luôn đồng biến R
\(2m^2-4m+7\)
\(=2m^2-4m+2+5\)
\(=2\left(m^2-2m+1\right)+5\)
\(=2\left(m-1\right)^2+5>=5>0\forall m\)
Do đó: Hàm số \(y=\left(2m^2-4m+7\right)x+3m^2-m-1\) luôn đồng biến trên R
Đúng 1
Bình luận (0)
cho hàm số y=(m2 - 2m +3)x +4 (d)
a) chứng tỏ hàm số luôn đồng biến với mọi m ?
b) chứng minh rằng khi m thay đổi các đường thẳng (đ) luôn đi qua 1 điểm cố định ?
Bài 1: Cho hàm số y=(\(m^2\)+1)x-5
a, Chứng tỏ rằng hàm số y là hàm số bậc nhất
b, Hàm số là hàm đồng biến hay ngoại biến?
Bài 2: Cho hàm số bậc nhất y=(m+3)x+7
a, Tìm m để hàm số là hàm số đồng biến
b, Tìm m để hàm số là hàm số đồng biến
Mong mọi người trả lời hai bài này giúp mình, mình cần gấp vào 16/08
1:
a: m^2+1>=1>0 với mọi m
=>y=(m^2+1)x-5 luôn là hàm số bậc nhất
b: Do m^2+1>0 với mọi m
nên hàm số y=(m^2+1)x-5 đồng biến trên R
Đúng 1
Bình luận (0)
Cho hàm số y=(m2 -2m+3)x - 4 (d)
chứng minh rằng với mọi m hàm số luôn đồng biến trên tập xác định của nó
Cho hàm số bậc nhất y=f(x)=(m^2+m+1)x+5.Chứng minh rằng:hàm số luôn đồng biến trên R
`a=m^2+m+1=m^2+2.m. 1/2 + (1/2)^2 + 3/4= (m+1/2)^2 + 3/4 >0 forall m`
`=> a>0 =>` Hàm số luôn đồng biến trên `RR`.
Đúng 2
Bình luận (2)
Để hàm số trên đồng biến khi \(m^2+m+1=m^2+m+\dfrac{1}{4}+\dfrac{3}{4}=\left(m+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\)
Vậy hàm số luôn đồng biến trên R
Đúng 2
Bình luận (1)
Ta có: \(m^2+m+1\)
\(=m^2+2\cdot m\cdot\dfrac{1}{2}+\dfrac{1}{4}+\dfrac{3}{4}\)
\(=\left(m+\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\forall m\)
Do đó: Hàm số \(f\left(x\right)=\left(m^2+m+1\right)x+5\) luôn đồng biến trên R
Đúng 1
Bình luận (1)
Cho hàm số bậc nhất : y=(m^2+1)x-1
a, Hàm số đã cho đồng biến hay nghịch biến ? Vì sao
b, Chứng tỏ rằng đồ thị hàm số đã cho luôn đi qua 1 điểm cố định ( x0;y0) với mọi m
Câu a :))
Hàm số đã cho đồng biến .
giải thích :
Do \(m^2\ge0\forall m\)
\(\Rightarrow m^2+1>0\)
Vậy hàm số trên đồng biến.
Đúng 0
Bình luận (0)
Giả sử đths đi qua điểm cố định ( x0;y0 )
Ta có y0 = ( m2 +1 )x0 - 1
<=> y0 = m2 x0 +x0 -1
<=> y0 -x0 +1 -m2x0 = 0
Để pt nghiệm đúng với mọi m \(\Leftrightarrow\hept{\begin{cases}y_0-x_0+1=0\\x_0=0\end{cases}\Leftrightarrow\hept{\begin{cases}y_0=-1\\x_0=0\end{cases}}}\)
Vậy đths luôn đi qua điểm cố định ( 0 ; -1 )
Đúng 0
Bình luận (0)
Cho hàm số \(y=\left(3m^2-7m+5\right)x-2011\). Chứng minh rằng hàm số trên luôn đồng biến trên R với mọi m
Cho hàm số y = m x - 1 2 x + m
Chứng minh rằng với mọi giá trị của tham số m, hàm số luôn đồng biến trên khoảng xác định của nó.
Với mọi tham số m ta có :
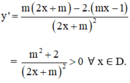
Vậy hàm số luôn đồng biến trên mỗi khoảng xác định của nó.
Đúng 0
Bình luận (0)