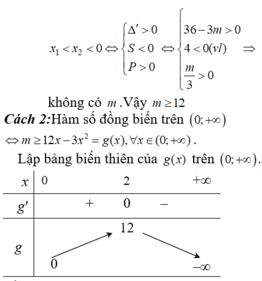
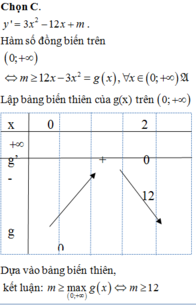
Tìm nghiệm của Mx=-x3-6x2+4

Những câu hỏi liên quan
Tìm tất cả các giá trị thực của tham số m sao cho hàm số
y
x
3
-
6
x
2
+
m
x
+
1
đồng biến trên khoảng
(
0
;
+
∞
)
? A.
m
≤
0
B.
m
≤
12
C.
m
≥
0...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x 3 - 6 x 2 + m x + 1 đồng biến trên khoảng ( 0 ; + ∞ ) ?
A. m ≤ 0
B. m ≤ 12
C. m ≥ 0
D. m ≥ 12
Tìm tất cả các giá trị thực của tham số m sao cho hàm số y = x 3 - 6 x 2 + m x + 1 đồng biến trên khoảng (0;+∞)?
A. m ≤ 0.
B. m ≤ 12.
C. m ≥ 0.
D. m ≥ 12.
Chọn D.
Cách 1: Tập xác định: D = R. Ta có ![]()
+) Trường hợp 1:
![]()
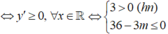
![]()
+) Trường hợp 2: Hàm số đồng biến trên (0; +∞) ⇔ y' = 0 có hai nghiệm x1; x2 thỏa mãn x1 < x2 ≤ 0(*)
-) Trường hợp 2.1: y’ = 0 có nghiệm x = 0 suy ra m = 0.
Nghiệm còn lại của y’ = 0 là x = 4 (không thỏa (*))
-) Trường hợp 2.2: y’ = 0 có hai nghiệm x1; x2 thỏa mãn:
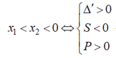
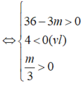
![]()
Kết hợp 2 trường hợp, vậy m ≥ 12
![]()
![]()
![]()
Đúng 0
Bình luận (0)
Cho hàm số
y
-
x
3
+
6
x
2
-
9
x
+
4
là bảng biến thiên như hình bên dướiCác giá trị của tham số m sao cho phương trình
-
x
3
+
6
x
2
-
9
x
-
m
0
có ba nghiệm phân biệt là A. -3 m 1 B. 0 m 4 C. -4 m 0 D. 1 m...
Đọc tiếp
Cho hàm số y = - x 3 + 6 x 2 - 9 x + 4 là bảng biến thiên như hình bên dưới
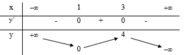
Các giá trị của tham số m sao cho phương trình - x 3 + 6 x 2 - 9 x - m = 0 có ba nghiệm phân biệt là
A. -3 < m < 1
B. 0 < m < 4
C. -4 < m < 0
D. 1 < m < 3
Hàm số
y
x
3
−
6
x
2
+
m
x
+
1
đồng biến trên
0
;
+
∞
khi giá trị của m là A.
m
≥
12
B.
m
≤
12
C.
m
≥
0
D.
m
≤...
Đọc tiếp
Hàm số y = x 3 − 6 x 2 + m x + 1 đồng biến trên 0 ; + ∞ khi giá trị của m là
A. m ≥ 12
B. m ≤ 12
C. m ≥ 0
D. m ≤ 0
Đáp án A
Ta có y ' = 3 x 2 − 12 x + m
Hàm số đồng biến trên y = f ' x
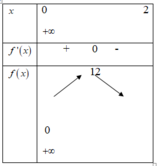
Ta có f ' x = − 6 x + 12 ⇒ f ' x = 0 ⇔ x = 2 . Ta có bảng biến thiên hàm số f(x) như trên
Từ bảng biến thiên, suy ra f x 0 ; + ∞ ≤ 12 ⇒ m ≥ f x 0 ; + ∞ ⇔ m ≥ 12
Đúng 0
Bình luận (0)
cho (d):y=mx và (p):y=x3-6x2+9x tìm m để d và p cắt nhau tại 3 điểm phân biệt điểm phân biệt
Pt hoành độ giao điểm:
\(x^3-6x^2+9x=mx\)
\(\Leftrightarrow x\left(x^2-6x+9-m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-6x+9-m=0\left(1\right)\end{matrix}\right.\)
d cắt (P) tại 3 điểm pb khi và chỉ khi (1) có 2 nghiệm pb khác 0
\(\Leftrightarrow\left[{}\begin{matrix}m\ne9\\\Delta'=9-\left(9-m\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m\ne9\\m>0\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Với giá trị nào của tham số m thì hàm số
y
x
3
-
6
x
2
+
m
x
+
1
đồng biến trên khoảng
0
;
+
∞...
Đọc tiếp
Với giá trị nào của tham số m thì hàm số y = x 3 - 6 x 2 + m x + 1 đồng biến trên khoảng 0 ; + ∞ ?
A. m ≥ 0
B. m ≤ 0
C. m ≥ 12
D. m ≤ 12
Với giá trị nào của tham số m thì hàm số y
x
3
-
6
x
2
+
m
x
+
1
đồng biến trên khoảng (0;+
∞
)? A. m
≥
0 B. m
≤
0 C. m
≥
12 D. m
≤
12
Đọc tiếp
Với giá trị nào của tham số m thì hàm số y = x 3 - 6 x 2 + m x + 1 đồng biến trên khoảng (0;+ ∞ )?
A. m ≥ 0
B. m ≤ 0
C. m ≥ 12
D. m ≤ 12
Chọn C.
![]() . Hàm số đồng biến trên (0;+
∞
)
. Hàm số đồng biến trên (0;+
∞
)![]() )
)
Lập bảng biến thiên của g(x) trên (0;+ ∞ )
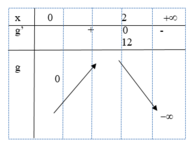
Dựa vào bảng biến thiên, kết luận ![]()
Lập bảng biến thiên của g(x) trên
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của tham số m để hàm số
y
x
3
-
6
x
2
+
m
x
-
1
có 5 điểm cực trị? A. 11. B. 15. C. 6. D. 8
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số m để hàm số y = x 3 - 6 x 2 + m x - 1 có 5 điểm cực trị?
A. 11.
B. 15.
C. 6.
D. 8
Có bao nhiêu giá trị nguyên của tham số ra để hàm số
y
x
3
-
6
x
2
+
m
x
-
1
có 5 điểm cực trị A. 11 B. 15 C. 6 D. 8
Đọc tiếp
Có bao nhiêu giá trị nguyên của tham số ra để hàm số y = x 3 - 6 x 2 + m x - 1 có 5 điểm cực trị
A. 11
B. 15
C. 6
D. 8
Chọn đáp án A
Hàm số đã cho có 5 điểm cực trị khi hàm số y = x 3 - 6 x 2 + m x - 1
có hai điểm cực x 1 , x 2 thỏa mãn x 1 > 0 , x 2 > 0
⇔ Phương trình y ' = 3 x 2 - 12 x + m = 0 có hai nghiệm dương phân biệt
Khi đó
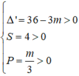
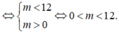
Do m ∈ 1 ; 2 ; 3 ; . . ; 11
Vậy có 11 giá trị m nguyên thỏa mãn yêu cầu bài toán
Đúng 0
Bình luận (0)
Có bao nhiêu giá trị nguyên của m tham số để hàm số y = x 3 − 6 x 2 + m x − 1 có 5 điểm cực trị.
A. 11
B. 15
C.6
D.8
Đáp án A
y = x 3 − 6 x 2 + m x − 1 ( 1) là hàm chẵn nên đồ thị hàm số đối xứng với nhau qua trục tung.
Đặt x = t , t ≥ 0 . Khi đó :
y = t 3 − 6 t 2 + m t − 1 (*)
Để hàm số (1) có 5 cực trị <=> hàm số (*) có 2 cực trị dương
⇔ y ' = 0 có 2 nghiệm dương phân biệt
⇔ 3 t 2 − 12 t + m = 0 có 2 nghiệm dương phân biết
⇔ Δ ' = 36 − 3 m > 0 12 2.3 > 0 3. m > 0 ⇔ 0 < m < 12
Đúng 0
Bình luận (0)