Question

Tìm tất cả các giá trị thực của tham số m sao cho hàm số  y = x 3 - 6 x 2 + m x + 1  đồng biến trên khoảng (0;+∞)?

A. m ≤ 0.

B. m ≤ 12.

C. m ≥ 0.

D. m ≥ 12.

Answer 1

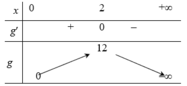
Chọn D.

Cách 1: Tập xác định: D = R. Ta có 

+) Trường hợp 1:

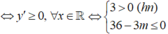
+) Trường hợp 2: Hàm số đồng biến trên (0; +∞) ⇔ y' = 0 có hai nghiệm x1; x2 thỏa mãn x1 < x2 ≤ 0(*)

-) Trường hợp 2.1: y’ = 0 có nghiệm x = 0 suy ra m = 0.

Nghiệm còn lại của y’ = 0 là x = 4 (không thỏa (*))

-) Trường hợp 2.2: y’ = 0 có hai nghiệm x1; x2 thỏa mãn:

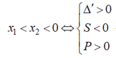
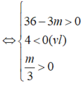
Kết hợp 2 trường hợp, vậy m ≥ 12