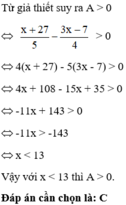tìm x để biểu thức sau có giá trị dương A=( x+5) .( x+9)

Những câu hỏi liên quan
bài tập :Tìm các giá trị của x để biểu thức sau có giá tị dương :
a) M=(x+5)(x+9)
b) Khi nào thì biểu thúc B=x^2-3x có giá trị dương
c) Tìm x để biểu thức A= x+3/x-1 có giá trị âm
(mọi người làm bảng xét dấu nhé)
Tìm các giá trị của x để cho biểu thức sau có giá trị dương : M = ( x + 5 ) ( x + 9 )
tìm giá trị của x để các biểu thức sau có giá trị dương:
a) (-2+2/5x +1 ) (x-2024)
b) x-2/x+5
a, F(\(x\)) = (-2 + \(\dfrac{2}{5}\)\(x\) + 1).(\(x\) - 2024)
-2 + \(\dfrac{2}{5}\)\(x\) + 1 = 0 ⇒ \(\dfrac{2}{5}\)\(x\) = 1 ⇒ \(x\) = \(\dfrac{5}{2}\);
\(x\) - \(2024\) = 0 ⇒ \(x\) = 2024
Lập bảng xét dấu ta có:
| \(x\) | \(\dfrac{5}{2}\) 2024 |
| \(x\) - 2024 | - - 0 + |
| - 2 + \(\dfrac{2}{5}\)\(x\) + 1 | - 0 + + |
| F(\(x\)) | + 0 - 0 + |
Theo bảng trên ta có: F(\(x\)) > 0 ⇔ \(\left[{}\begin{matrix}\dfrac{5}{2}>x\\2024< x\end{matrix}\right.\)
Đúng 0
Bình luận (0)
b,F(\(x\) ) = \(\dfrac{x-2}{x+5}\)
\(x\) - 2 = 0 ⇒ \(x\) = 2; \(x\) + 5 = 0 ⇒ \(x\) = -5
Lập bảng xét dấu ta có:
| \(x\) | -5 2 |
| \(x-2\) | - - 0 + |
| \(x+5\) | - 0 + 0 + |
| F(\(x\)) | + 0 - 0 + |
Theo bảng trên ta có: F(\(x\)) > 0 ⇔ \(\left[{}\begin{matrix}x< -5\\x>2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Câu 9: Chứng tỏ với mọi giá trị x,y thuộc Q thì giá trị của biểu thức sau luôn luôn là số dương :
M=3[x2+1]+x2y2+y2-2 / [x+y]2+5
Câu10:Tìm cặp số nuyên dương x;y để biểu thức sau có giá trị dương
A=2x+2y-3 / x+y
Tìm các giá trị x để các biểu thức sau có giá trị dương
a)x^2-7/9x
b)x-2/x+5
Cho biểu thức \(A=\frac{\sqrt{x}+1}{\sqrt{x}-1}\)
a) Tính giá trị biểu thức A tại x=\(\frac{16}{9}\) và x=\(\frac{25}{9}\)
b) Tìm giá trị x để A=5
c) Tìm xϵ Z để A có giá trị là một số nguyên dương
a)Tại \(x=\frac{16}{9}\) ta có: \(A=\frac{\sqrt{x}+1}{\sqrt{x}-1}=\frac{\sqrt{\frac{16}{9}}+1}{\sqrt{\frac{16}{9}}-1}=\frac{\frac{4}{3}+1}{\frac{4}{3}-1}=\frac{\frac{7}{3}}{\frac{1}{3}}=7\)
Tại \(x=\frac{25}{9}\) ta có: \(A=\frac{\sqrt{x}+1}{\sqrt{x}-1}=\frac{\sqrt{\frac{25}{9}}+1}{\sqrt{\frac{25}{9}}-1}=\frac{\frac{5}{3}+1}{\frac{5}{3}-1}=\frac{\frac{8}{3}}{\frac{2}{3}}=4\)
b)Khi \(A=5\Rightarrow\frac{\sqrt{x}+1}{\sqrt{x}-1}=5\)(*)
Đk:\(\sqrt{x}-1\ne0\Rightarrow x\ne1;\sqrt{x}\ge0\Rightarrow x\ge0\)
Đặt \(\sqrt{x}+1=t\left(t\ge0\right)\),(*) trở thành
\(\frac{t}{t-2}=5\Rightarrow t=5\left(t-2\right)\)
\(\Rightarrow t=5t-10\)
\(\Rightarrow2t=5\Rightarrow t=\frac{5}{2}\)(thỏa mãn)
\(t=\frac{5}{2}\Rightarrow\sqrt{x}+1=\frac{5}{2}\)
\(\Rightarrow\sqrt{x}=\frac{3}{2}\Leftrightarrow\sqrt{x^2}=\left(\frac{3}{2}\right)^2\Leftrightarrow x=\frac{9}{4}\)(thỏa mãn)
Vậy \(x=\frac{9}{4}\)
Đúng 1
Bình luận (0)
Tìm x để biểu thức sau có giá trị dương A = x + 27 5 − 3x − 7 4
A. x ≤ 13
B. x > 13
C. x < 13
D. x ≥ 13
tìm x để biểu thức sau có giá trị ko dương A=(x^2+1)(x-2)(x+3)
Để A có giá trị không dương hay \(A\le0\)
\(=>\left(x^2+1\right)\left(x-2\right)\left(x+3\right)\le0\)
\(=>\left(x-2\right)\left(x+3\right)\le0\) ( Vì : \(x^2+1\ge1>0\forall x\) )
\(=>\left\{{}\begin{matrix}x-2\le0\\x+3\ge0\end{matrix}\right.\) ( Vì : \(x+3>x-2\forall x\) )
\(=>\left\{{}\begin{matrix}x\le2\\x\ge-3\end{matrix}\right.\)
\(=>-3\le x\le2\)
Đúng 0
Bình luận (0)
A = (\(x^2\) + 1).(\(x-2\)).(\(x+3\)). Lập bảng xét dấu ta có:
| \(x\) | \(-3\) 2 |
| \(x^2\) + 1 | + + + + |
| \(x\) - 2 | - - 0 + |
| \(x\) + 3 | - 0 + + |
| A | + 0 - 0 + |
Theo bảng trên ta có: -3 ≤ \(x\) ≤ 2
Đúng 0
Bình luận (0)
Tìm giá trị của x để biểu thức A
5
−
2
x
x
2
+
4
có giá trị dương A. x 5/2 B. x 5/2 C. x 5/2 D. x 2
Đọc tiếp
Tìm giá trị của x để biểu thức A = 5 − 2 x x 2 + 4 có giá trị dương
A. x < 5/2
B. x > 5/2
C. x = 5/2
D. x > 2