Cho hình vuông ABCD, hãy nội tiếp hình vuông này bằng 1 tam giác đều MNP sao cho các đỉnh M;N;P lần lượt nằm trên các cạnh AD;CD;BC của hình vuông ?

Những câu hỏi liên quan
Cho S.ABC là hình chóp tam giác đều có các cạnh bên bằng a và có góc giữa các mặt bên và mặt phẳng đáy là α. Hình nón đỉnh S có đường tròn đáy nội tiếp tam giác đều ABC gọi là hình nón nội tiếp hình nón đã cho. Hãy tính diện tích xung quanh của hình nón này theo a và α
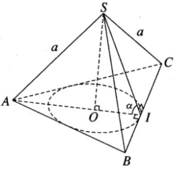
Gọi I là trung điểm của cạnh BC và O là tâm của tam giác đều ABC. Theo giả thiết ta có SA = SB = SC = a và ∠ SIO = α. Đặt OI = r, SO = h, ta có AO = 2r và

Do đó a 2 = r 2 tan 2 α + 4 r 2 = r 2 tan 2 α + 4
Vậy 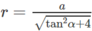
Hình nón nội tiếp có đường sinh là :
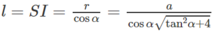
Diện tích xung quanh của hình nón nội tiếp hình chóp S.ABC là:
![]()
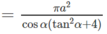
Đúng 0
Bình luận (0)
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng 2a. Diện tích xung quanh của hình nón đỉnh S và đáy là hình tròn nội tiếp hình vuông ABCD bằng A.
π
a
2
17
4
B.
π
a
2
15
4
C. ...
Đọc tiếp
Cho hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a và chiều cao bằng 2a. Diện tích xung quanh của hình nón đỉnh S và đáy là hình tròn nội tiếp hình vuông ABCD bằng
A. π a 2 17 4
B. π a 2 15 4
C. π a 2 15 2
D. π a 2 17 2
Câu 1: Một hình vuông và 1 tam giác đều cùng nội tiếp trong một đường tròn (O;1) sao cho một cạnh của tam giác song song với một cạnh của hình vuông. tính diện tích phần chung của tam giác và hình vuông. Câu 2: Cho tứ giác ABCD nội tiếp dường tròn tâm O. Cho biết phân giác của các góc BAD và ABC cắt nhau tại một điểm E trên CD.a Cm: AD+BCCDB Cho biết CD/CBk1 tính S ADE/ S BCE
Đọc tiếp
Câu 1: Một hình vuông và 1 tam giác đều cùng nội tiếp trong một đường tròn (O;1) sao cho một cạnh của tam giác song song với một cạnh của hình vuông. tính diện tích phần chung của tam giác và hình vuông.
Câu 2: Cho tứ giác ABCD nội tiếp dường tròn tâm O. Cho biết phân giác của các góc BAD và ABC cắt nhau tại một điểm E trên CD.
a> Cm: AD+BC=CD
B> Cho biết CD/CB=k>1 tính S ADE/ S BCE
Cho một hình vuông có cạnh bằng 4. Chia hình vuông này thành 16 hình vuông đơn vị có cạnh bằng 1. Hỏi có bao nhiêu tam giác có các đỉnh là các đỉnh của hình vuông đơn vị?
A. 2248
B. 2148
C. 2160
D. 2168
Chọn B
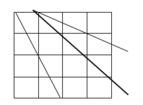
Số cách chọn ra 3 đỉnh trong số 25 đỉnh của các hình vuông đơn vị là: C 25 3
TH1: 3 đỉnh nằm trên cùng 1 hàng hoặc cùng 1 cột là: 5 C 5 3 + 5 C 5 3
TH2: 3 đỉnh nằm trên một trong các đường chéo của hình vuông kích thước 4x4, 3x3, 2x2 sao cho các đường chéo ấy không trùng nhau là ![]()
TH3: 3 đỉnh nằm trên một trong các đường chéo của hình chữ nhật kích thước 2x4. Số hình chữ nhật đó là 6. Do đó số cách chọn là 12
Vậy số tam giác được tạo thành là ![]() = 2148
= 2148
Đúng 0
Bình luận (0)
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
Đọc tiếp
Cho hình vuông ABCD nội tiếp đường tròn tâm O, bán kính R và GEF là tam giác đều nội tiếp đường tròn đó, EF là dây song song với AB (h.119). Cho hình đó quay quanh trục GO. Chứng minh rằng:
Bình phương thể tích của hình trụ sinh ra bởi hình vuông bằng tích của thể tích hình cầu sinh ra bởi hình tròn và thể tích hình nón do tam giác đều sinh ra.
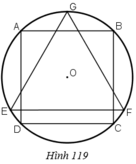
Dựng GH vuông góc EF.
Khi hình vẽ quay quanh trục GO thì:
Ta có:
AB = BC ![]()
Thể tích hình trụ sinh ra bởi hình vuông ABCD là:

Thể tích hình nón:
![]()
![]()
Đúng 0
Bình luận (0)
Cho hình vuông ABCD. Trong hình vuông lấy điểm M sao cho góc MAB bằng góc MBA bằng 18 độ. Chứng minh rằng: tam giác MCD là tam giác đều
Cho hình vuông ABCD , các điểm M, N thay đổi lần lượt nằm trên các cạnh BC, CD sao cho \(\widehat{MAN}=45^0\)(M,. N không trùng với các đỉnh của hình vuông). Gọi P, Q lần lượt là giao điểm của AM, AN với BD.
1) Chứng minh rằng: Tứ giác ABMQ là tứ giác nội tiếp.
2) Chứng minh rằng: Tỉ số diện tích của APQ và tam giác ANM không đổi
Cho hình vuông ABCD . Lấy điểm M ở miền trong hình vuông sao cho góc MCD bằng góc MCDvà bằng 15 độ . Chứng minh rằng tam giác MAB là tam giác đều
Cho hình vuông ABCD có cạnh dài 18cm . Trên các cạnh AB , BC , CD lần lượt lấy các điểm M, N, P sao cho AM = BN = DP và bằng 1/3canhj hình vuông . Tính diện tích tam giác MNP
(Giải giúp tôi nhé , nhớ viết lời giải nhé )😂😂😂😂









