 Giải dùm em bài 1,2,3,4,5 với ạ
Giải dùm em bài 1,2,3,4,5 với ạ
Giải dùm em bài 4 với ạ
 giải dùm em bài 4 với ạ
giải dùm em bài 4 với ạ
Giải dùm em bài 9 với ạ em cảm ơn
9.
Gọi H là trung điểm AB \(\Rightarrow A'H\perp\left(ABCD\right)\Rightarrow\widehat{A'CH}=45^0\)
\(CH=\sqrt{BH^2+BC^2}=\sqrt{\left(\dfrac{2a}{2}\right)^2+a^2}=a\sqrt{2}\)
\(\Rightarrow A'H=CH.tan45^0=a\sqrt{2}\)
\(V=A'H.AB.AD=2a^3\sqrt{2}\)
b.
Ta có: \(DD'||AA'\Rightarrow DD'||\left(AA'C\right)\)
\(\Rightarrow d\left(DD';A'C\right)=d\left(DD';\left(AA'C\right)\right)=d\left(D;\left(AA'C\right)\right)\)
Trong mp (ABCD), nối DH cắt AC tại E \(\Rightarrow DH\cap\left(AA'C\right)=E\)
Áp dụng định lý Talet: \(\dfrac{EH}{DE}=\dfrac{AH}{DC}=\dfrac{1}{2}\Rightarrow DE=2EH\)
\(\Rightarrow d\left(D;\left(AA'C\right)\right)=2d\left(H;\left(AA'C\right)\right)\)
Kẻ \(HF\perp AC\Rightarrow AC\perp\left(AHF\right)\)
Trong tam giác vuông AHF, kẻ \(HK\perp A'F\Rightarrow HK\perp\left(AA'C\right)\Rightarrow HK=d\left(H;\left(AA'C\right)\right)\)
Ta có: \(HF=AH.sin\widehat{BAC}=\dfrac{AH.BC}{AC}=\dfrac{AH.BC}{\sqrt{AB^2+AD^2}}=\dfrac{a\sqrt{5}}{5}\)
Áp dụng hệ thức lượng:
\(\dfrac{1}{HK^2}=\dfrac{1}{HF^2}+\dfrac{1}{A'H^2}=\dfrac{11}{2a^2}\Rightarrow HK=\dfrac{a\sqrt{22}}{11}\)
\(\Rightarrow d\left(DD';A'C\right)=2HK=\dfrac{2a\sqrt{22}}{11}\)
dạ giải dùm em bài 1 phần tự luận với ạ, em đang cần gấp ạ:
Giải dùm em bài này với ạ : (m+1)^2 >=4m
\(\left(m+1\right)^2\ge4m\Leftrightarrow m^2+2m+1\ge4m\Leftrightarrow m^2-2m+1\ge0\)\(\Leftrightarrow\left(m-1\right)^2\ge0\)
Vì \(\left(m-1\right)^2\ge0\)(luôn đúng) nên pt vô số nghiêmj
Mình cũng ko bt đây là giải pt hay cm BĐT nữa nên nếu ko đúng mục đích thì bạn thông cảm
Giải dùm em bài này ạ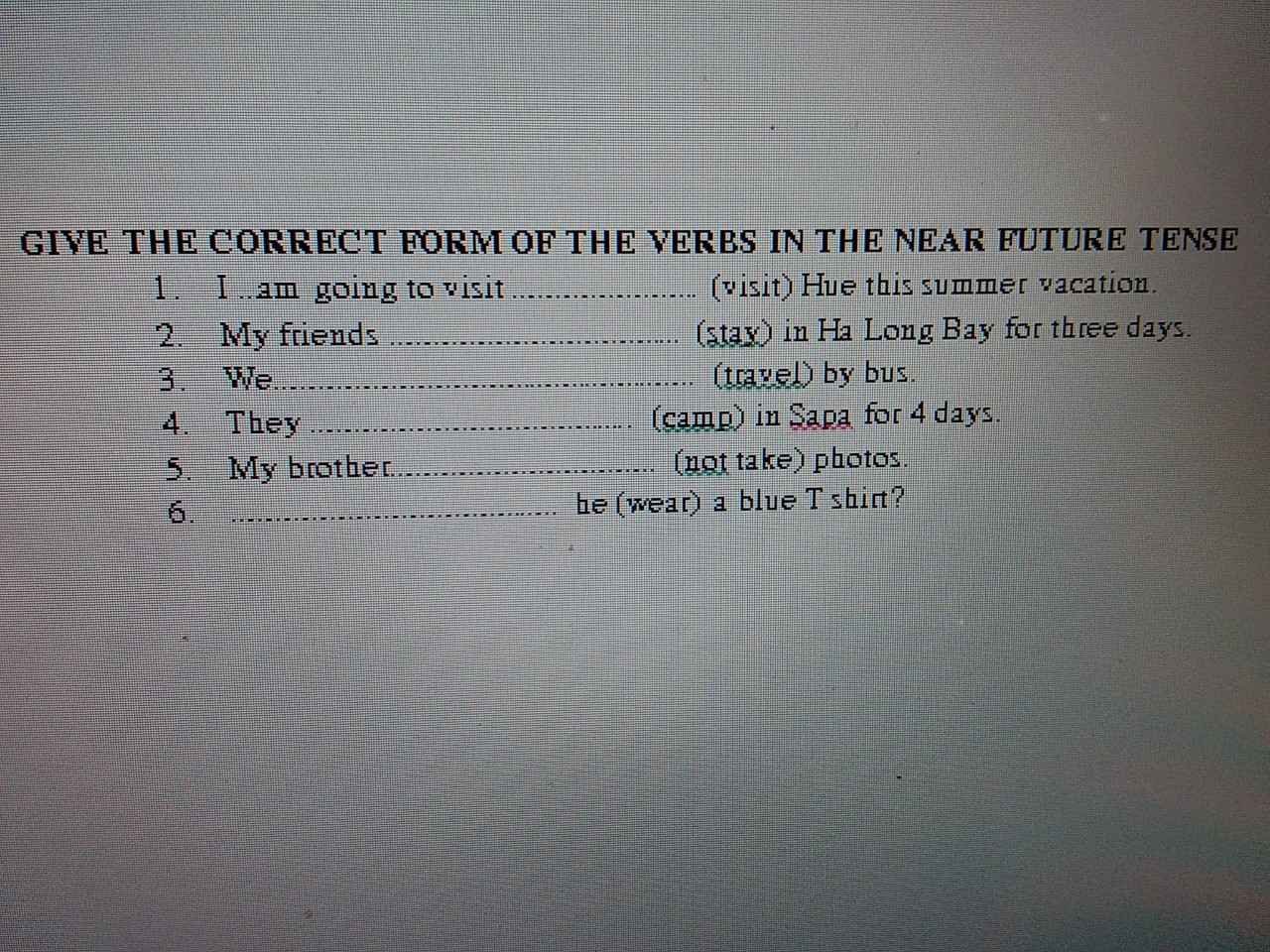
are going to stay
are going to travel
are going to camp
aren't going to take
Is he going to

Giải dùm em bài 3 ạ
Chọn 2 bạn bất kì từ 32 bạn: \(C_{32}^2\) cách
Chọn 2 bạn bất kì trong đó ko có mặt cả Ưu và Tiên (nghĩa là chọn 2 bạn trong 30 bạn còn lại): \(C_{30}^2\) cách
Số cách thỏa mãn: \(C_{32}^2-C_{30}^2=...\)
Giải dùm em bài 6 ạ em đang gấp

Ai giải dùm em bài này em cảm ơn ạ!
