Chứng minh rằng :1110 -1 chia hết cho 100 .

Những câu hỏi liên quan
Chứng minh rằng: 11 10 – 1 chia hết cho 100
Ta có; 1110 = (10+1)10 ( khai triển nhị thức Niu- tơn )
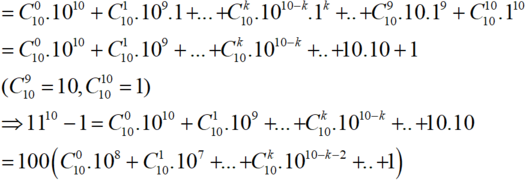
Do đó 1110 -1 chia hết cho 100
Đúng 0
Bình luận (0)
Chứng minh rằng:
a. 1110 - 1 chia hết cho 100
b. 9 . 10n + 18 chia hết cho 27
c. 16n - 15n - 1 chia hết cho 255
Chứng minh rằng: 2^100 - 1 chia hết cho 125.
Chứng minh rằng: 11^100-1 chia hết cho 100
Ta có : \(11^{10}⋮1\left(mod100\right)\)
\(\Rightarrow\left(11^{10}\right)^{10}⋮1\left(mod100\right)\)
\(\Rightarrow11^{100}⋮1\left(mod100\right)\)
\(1⋮1\left(mod100\right)\)
\(\Rightarrow11^{100}-1⋮0\left(mod100\right)\)
Hay \(11^{100}-1⋮100\)( dpcm )
Đúng 0
Bình luận (0)
Chứng minh rằng: (11^ 10 -1) chia hết cho 100
1110-1=(1+10)10-1=(1+c11010+c210102+...+c910109+1010)-1
=102+c210102+...+c910109+1010
tổng sau cùng chia hết cho 100 => 1110-1chia hết cho 100
CHÚC BẠN HỌC GIỎI
TK MÌNH NHÉ
Đúng 0
Bình luận (0)
Chứng minh rằng 2^100 -1 chia hết cho 125
chứng minh rằng: b*1010+c*100+a*1 chia hết cho 4 với a,b,c nằm trong tập hợp N và a+b*2chia hết cho 4chứng minh rằng: b*1010+c*100+a*1 chia hết cho 4 với a,b,c nằm trong tập hợp N và a+b*2chia hết cho 4
ai trả lời nhanh thì tôi k cho nhiều nhất
Đúng 0
Bình luận (0)
Bài 1: Cho S= 3 + 3^2 + 3^3 +...+ 3^100. Chứng minh rằng S chia hết cho 4. Tìm chữ số tận cùng của S.
Bài 2: Chứng minh rằng: ( 1+2+2^2+2^3+...+2^17) chia hết cho 9
Bài 1: Cho S= 3 + 3^2 +3^3 +...+3^100. Chứng minh rằng S chia hết cho 4. Tìm chữ số tận cùng của S.
Bài 2: Chứng minh rằng: ( 1 + 2 + 2^2 + 2^3 +...+ 2^17 ) chia hết cho 9
chứng minh rằng: A= 1+2+3+...+99+100 chia hết cho 2
\(A=\dfrac{\left(100+1\right)\cdot100}{2}=101\cdot50⋮2\)
Đúng 0
Bình luận (0)
A=(1+100).100:2
A= 5050
Vì 5050:2=2525
=> A chia hết cho 2
Đúng 0
Bình luận (0)

















