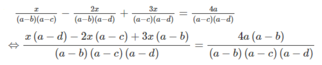
⇔ x(a − d) − 2x(a − c) + 3x(a − b) = 4a(a − b)

⇔ x(a − d − 2a + 2c + 3a − 3b) = 4a(a − b)

⇔ x(2a − 3b + 2c − d) = 4a(a − b)

Theo giả thiết, b + d = 2c nên 2a – 3b + 2c – d = 2a – 2b = 2 (a – b ).

Do đó phương trình đã cho tương đương với phương trình 2(a − b)x = 4a(a − b)

Để ý rằng a – b ≠ 0, ta thấy ngay phương trình cuối có nghiệm duy nhất x = 2a.

Vậy phương trình đã cho cũng có nghiệm duy nhất x = 2a.

Đặt \(A=4a^2+4a+15\)

\(\Rightarrow A=4a\left(a+1\right)+15\)

\(a\left(a+1\right)⋮2\)( vì a và a+1 là 2 số tự nhiên liên tiếp)

\(\Rightarrow4a\left(a+1\right)⋮8\\ \)

Mà 15 chia 8 dư 7

\(\Rightarrow A\) chia 8 dư 7

\(\Rightarrow A\) không là số chính phương vì số chính phương chia 8 dư 0 ,1,4

\(\Rightarrow a\in\varnothing\)

Đặt: \(4a^2+4a+15=k^2\left(k\in N\right)\)

\(\Rightarrow4a^2+2a+2a+1+14=k^2\)

\(\Rightarrow2a\left(2a+1\right)+\left(2a+1\right)+14=k^2\)

\(\Rightarrow\left(2a+1\right)\left(2a+1\right)+14=k^2\)

\(\Rightarrow\left(2a+1\right)^2-k^2=-14\) ( * )

Ta sẽ chứng minh: \(a^2-b^2=\left(a-b\right)\left(a+b\right)\)

Thật vậy, ta có: \(a^2-b^2=a^2-ab+ab-b^2=a\left(a-b\right)+b\left(a-b\right)=\left(a-b\right)\left(a+b\right)\)

\(\RightarrowĐpcm\)

Áp dụng vào (*), có: \(\left(2a+1-k\right)\left(2a+1+k\right)=-14\)

Vì \(a,k\in N\) nên \(2a+1+k\in N\)

\(\Rightarrow2a+1-k,2a+1+k\inƯ\left(14\right)\)
Có: \(-14=\left(-14\right).1=\left(-7\right).2=\left(-2\right).7=\left(-1\right).14\)

Mặt khác, \(2a+1-k,2a+1+k\) là hai số cùng tính chẵn lẻ mà ta thấy khi phân tích \(-14\) thành thừa số nguyên tố thì nó đều là tích của một số chẵn và một số lẻ

\(\Rightarrow\) Không tồn tại \(a\) và \(k\) thỏa mãn.

Vậy không tồn tại \(a\) thỏa mãn đề bài.