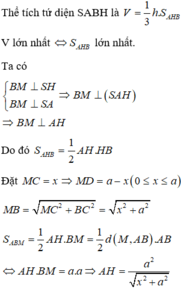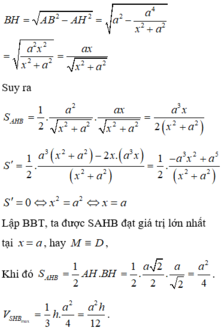Cho hình vuông ABCD có điểm M nằm trên cạnh CD, Đường thảng qua M vuông góc với BM cắt AD tại điểm N. Tìm vị trí của M để đoạn DN đạt giá trị lớn nhất ?

Những câu hỏi liên quan
cho hình vuông ABCD có cạnh bằng a. trên cạnh BC lấy điểm E, qua A kẻ đuờng thẳng vuông góc với AE, cắt CD tại F. I là trung điểm của EF, AI cắt CD tại K . CMinh AEF là tam giác vuông cân và KE KF. D,I,B thẳng hàng . trên AB lấy điểm M sao cho BE BM, tìm vị trí của E trên BC để tam giác DEM đạt giá trị lớn nhất
a/
Ta có
\(\widehat{BAE}+\widehat{DAE}=\widehat{ABC}=90^o\)
\(\widehat{FAD}+\widehat{DAE}=\widehat{FAE}=90^o\)
\(\Rightarrow\widehat{BAE}=\widehat{FAD}\)(1)
Ta có \(AB=AD\) (2)
Xét tg vuông BAE và tg vuông DAF
Từ (1) và (2) \(\Rightarrow\Delta BAE=\Delta DAF\) (hai tg vuông có cạnh góc vuông và góc nhọn tương ứng bằng nhau)
\(\Rightarrow AE=AF\Rightarrow\Delta AEF\) cân tại A
Mà \(\widehat{FAE}=90^o\Rightarrow\Delta AEF\) vuông cân tại A
Xét \(\Delta AEF\) có
IE=IF
\(\Rightarrow AD\perp EF\) (trong tg cân đường trung tuyến xp từ đỉnh đồng thời là đường cao)
Xét \(\Delta KEF\) có
IE=IF; \(AD\perp EF\)
\(\Rightarrow\Delta KEF\) là tg cân (trong tg đường cao xp từ đỉnh đồng thời là đường trung tuyến thì tg đó là tg cân) \(\Rightarrow KE=KF\)
b/
Ta có \(\Delta AEF\) vuông cân tại A \(\Rightarrow\widehat{AFE}=\widehat{AEF}=45^o\) (1)
Xét \(\Delta ABD\) có
AB=AD; \(\widehat{BAD}=90^o\Rightarrow\Delta ABD\) vuông cân tại A \(\Rightarrow\widehat{ADB}=\widehat{ABD}=45^o\) (2)
Từ (1) và (2) \(\Rightarrow\widehat{ADB}=\widehat{AEF}\) (3)
Gọi P là giao của AD với EF; Q là giao của BD với AE
Xét \(\Delta AFP\) và \(\Delta ABQ\) có
AD=AB
\(\Delta AEF\) cân tại A => AF=AE
\(\widehat{DAF}=\widehat{BAE}\left(cmt\right)\)
\(\Rightarrow\Delta AFP=\Delta ABQ\left(c.g.c\right)\Rightarrow\widehat{APF}=\widehat{AQB}\)
Mà \(\widehat{APF}=\widehat{DPI};\widehat{AQB}=\widehat{EQI}\) (góc đối đỉnh)
\(\Rightarrow\widehat{DPI}=\widehat{EQI}\) (4)
Nối D với I, B với I. Xét \(\Delta DPI\) và \(\Delta EQI\)
Từ (3) và (4) \(\Rightarrow\widehat{DIP}=\widehat{EIQ}\)
Mà \(\widehat{EIQ}+\widehat{FIB}=\widehat{FIE}=180^o\)
\(\Rightarrow\widehat{DIP}+\widehat{FIB}=\widehat{DIB}=180^o\) => D; I; B thẳng hàng
c/
Ta có \(AM=AB-BM;CE=BC-BE\)
Mà \(BM=BE;AB=BC\)
\(\Rightarrow AM=CE\)
Ta có AD=CD
\(S_{\Delta ADM}=\frac{AD.AM}{2}=S_{\Delta CDE}=\frac{CD.CE}{2}\Rightarrow S_{\Delta ADM}+S_{\Delta CDE}=2S_{\Delta CDE}=CD.CE\)
\(S_{\Delta BME}=\frac{BE.BM}{2}=\frac{BE^2}{2}\)
Gọi a là cạnh hình vuông ABCD có
\(S_{\Delta DEM}=S_{ABCD}-\left(S_{\Delta ADM}+S_{\Delta CDE}+S_{BME}\right)=\)
\(=a^2-2S_{\Delta CDE}-\frac{BE^2}{2}=a^2-a.CE-\frac{\left(a-CE\right)^2}{2}=\)
\(=\frac{2a^2-2a.CE-a^2+2a.CE-CE^2}{2}=\frac{a^2-CE^2}{2}\)
\(\Rightarrow S_{\Delta DEM}\) lớn nhất khi \(a^2-CE^2\) lớn nhất \(\Rightarrow CE^2\) nhỏ nhất => CE nhỏ nhất
CE nhỏ nhất khi CE=0 => E trùng C
cho hình vuông ABCD có cạnh bằng a. trên cạnh BC lấy điểm E, qua A kẻ đuờng thẳng vuông góc với AE, cắt CD tại F. I là trung điểm của EF, AI cắt CD tại K . CMinh
(AEF là tam giác vuông cân và KE=KF. D,I,B thẳng hàng).
(trên AB lấy điểm M sao cho BE=BM, tìm vị trí của E trên BC để tam giác DEM đạt giá trị lớn nhất
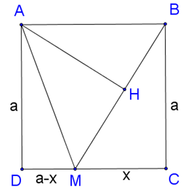
Cho mình hỏi bài với! Cho hình vuông ABCD.Có 1 cạnh=20cm.Trên CD lấy M ,đặt CM=x(0<x<20). Đường vuông góc BM tại M cắt AD tại N.
a)Tính DN biết MC=5cm.
b) Tìm vị trí của M để DN lớn nhất.
a, có ABCD là hình vuông=>\(AB=BC=CD=AD=20cm\)
\(=>DM=DC-MC=20-5=15cm\)
xét \(\Delta BMN\) vuông tại M\(=>BM=\sqrt{BC^2+MC^2}=\sqrt{20^2+5^2}=5\sqrt{17}cm\)
có: \(BN^2-NM^2=BM^2=425\)
\(< =>AB^2+AN^2\)\(-\left(ND^2+DM^2\right)\)\(=425\)
\(< =>20^2+\left(20-ND\right)^2-ND^2-15^2=425=>ND=3,75cm\)
b, như ý a, ta có: \(BM^2=x^2+20^2\)(CM=x)
\(=>DM=20-x\)
có từ ý a
\(=>BM^2=BN^2-NM^2\)
\(=>x^2+20^2=20^2+\left(20-ND\right)^2-\left(ND^2+DM^2\right)\)
\(x^2+20^2=20^2+\left(20-ND\right)^2\)\(-\left[ND^2+\left(20-x\right)^2\right]\)
\(< =>x^2+20^2=20^2\)\(-40ND+ND^2-ND^2-\left(20-x\right)^2\)
\(< =>x^2+20^2=-40ND+40x-x^2\)
\(< =>40ND=40x-x^2-x^2-20^2\)
\(=>ND=\dfrac{-2x^2+40x-400}{40}=\dfrac{-\left(x^2-20x+200\right)}{20}\)
có \(x^2-20x+200=x^2-2.10x+10^2-10^2+200=\left(x-10\right)^2+100\ge100\)
\(=>\left(-x^2-20x+200\right)\le100\) Dấu= xảy ra<=>x=10<=>MC=10cm
<=>M là trung điểm CD
Đúng 1
Bình luận (2)
Cho hình thang ABCD vuông tại C và D có AD = 3, BC = 4 và CD = 5. M là điểm di động trên cạnh CD. Tìm vị trí của điểm M để tổng AM + MB đạt giá trị nhỏ nhất
cho hình vuông ABCD có cạnh bằng a. Trên cạnh BC lấy điểm E, qua A kẻ kẻ đường thẳng vuông góc với AE, đường thẳng này cắt đường thẳng CD tại EF. Gọi I là trung điểm của EF, AI cắt CD tại K1/ cHỨNG MINH: A/ tam giác AEF là tam giác vuông cân và KEKFb/ Ba điểm D, I, B thẳng hàng2/ Trên cạnh AB lấy điểm M sao cho BEBM. Tìm vị trí ủa điểm E trên cạnh BC để diện tích tam giác DEM đạt giá trị lớn nhấtgiúp mk nhakhoảng 9 h có nhagấp lắm
Đọc tiếp
cho hình vuông ABCD có cạnh bằng a. Trên cạnh BC lấy điểm E, qua A kẻ kẻ đường thẳng vuông góc với AE, đường thẳng này cắt đường thẳng CD tại EF. Gọi I là trung điểm của EF, AI cắt CD tại K
1/ cHỨNG MINH: A/ tam giác AEF là tam giác vuông cân và KE=KF
b/ Ba điểm D, I, B thẳng hàng
2/ Trên cạnh AB lấy điểm M sao cho BE=BM. Tìm vị trí ủa điểm E trên cạnh BC để diện tích tam giác DEM đạt giá trị lớn nhất
giúp mk nha
khoảng 9 h có nha
gấp lắm
1/A/vì AF\(\perp\)AE
=>AEF là tam giác vuông
vì ABCD là hình vuông
=> AB=AD ;góc B=góc D=90 độ
=>ABE và ADF là 2 tam giác vuông tại góc B và góc D
ta có:
góc FAD + góc DAE=90 độ
góc DAE+góc EAB=90 độ
=>góc FAD=góc EAB
xét 2 tam giác vuông ABE và ADF có:
AB =AD
góc FAD =góc EAB
=> ΔABE=ΔADF
=>AF=AE
=>ΔAEF là tam giác vuông cân
trong tam giác AFE có:
AF=AE
I là trung điểm của EF
=>AI là đg trung trực của EF
=>IK là đg trung trực của EF
=>KF=KE
mk chỉ làm đến đó thui nha
thấy đúng thì click cho mk
![]()
Đúng 0
Bình luận (2)
Cho đoạn thẳng CD=6 cm, I là một điểm nằm giữa C và D (IC>ID).Trên tia Ix vuông góc với CD lấy 2 điểm M và N sao cho IC=IM,ID=IN, CD cắt MD tại K( K thuộc MD),DN cắt MC tại L(L thuộc MC). Tìm vị trí cuả điểm I trên CD sao cho CN.NK có giá trị lớn nhất.
cho tam giác ABC vuông cân tại A có ABACa trung tuyến AD, M là 1 điểm di động trên AD. Gọi N và P lần lượt là hình chiếu vuông góc của M trên các cạnh AB và AC. PD cắt tia Bx vuông góc với AB ở điểm E. Gọi H là hình chiếu của N trên PD.a) chứng minh 3 điểm B,M,H thẳng hàng b) xác định vị trí điểm M để tam giác AHB có diện tích lớn nhất tính giá trị lớn nhất đó c) chứng tỏ khi M di động, đường thẳng HN luôn đi qua 1 điểm cố định .Tìm vị trí của M để HN dài nhất( giải 1 câu là đc rồi cảm ơn mấy me...
Đọc tiếp
cho tam giác ABC vuông cân tại A có AB=AC=a trung tuyến AD, M là 1 điểm di động trên AD. Gọi N và P lần lượt là hình chiếu vuông góc của M trên các cạnh AB và AC. PD cắt tia Bx vuông góc với AB ở điểm E. Gọi H là hình chiếu của N trên PD.
a) chứng minh 3 điểm B,M,H thẳng hàng
b) xác định vị trí điểm M để tam giác AHB có diện tích lớn nhất tính giá trị lớn nhất đó
c) chứng tỏ khi M di động, đường thẳng HN luôn đi qua 1 điểm cố định .Tìm vị trí của M để HN dài nhất
( giải 1 câu là đc rồi cảm ơn mấy mem )
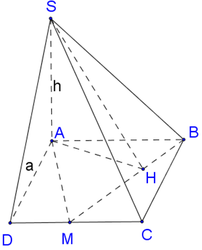
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh
a
,
SA
h
vuông góc với mặt phẳng (ABCD). Gọi M là điểm thay đổi trên cạnh CD. Kẻ SH vuông góc với BM tại H. Thể tích tứ diện S.ABH đạt giá trị lớn nhất là A.
a
2
h
12
B.
a
2...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh a , SA = h vuông góc với mặt phẳng (ABCD). Gọi M là điểm thay đổi trên cạnh CD. Kẻ SH vuông góc với BM tại H. Thể tích tứ diện S.ABH đạt giá trị lớn nhất là
A. a 2 h 12
B. a 2 h 24
C. a 2 h 6
D. a 2 h 18
1/ Cho hình vuông ABCD. Lấy M tùy ý trên cạnh BC. Đường thẳng vuông góc AM tại M, cắt CD tại N. Tìm vị trí của M để CN lớn nhất2/ Cho hình vuông ABCD. Lấy M,N,P,Q thuộc 4 cạnh AB,BC,CD,AD. TÌm điều kiện của tứ giác MNPQ để chu vi tứ giác MNPQ nhỏ nhất3/ Lấy I nằm trong tam giác ABC nhọn. Vẽ IH⊥BC,IK⊥AC,IL⊥AB. Xác định vị trí của I để AL^2+BH^2+CK^2 nhỏ nhất4/ Cho tam giác ABC nhọn. Tìm điểm M trong tam giác sao cho AM.BC+BM.AC+CM.AB nhỏ nhất
Đọc tiếp
1/ Cho hình vuông ABCD. Lấy M tùy ý trên cạnh BC. Đường thẳng vuông góc AM tại M, cắt CD tại N. Tìm vị trí của M để CN lớn nhất
2/ Cho hình vuông ABCD. Lấy M,N,P,Q thuộc 4 cạnh AB,BC,CD,AD. TÌm điều kiện của tứ giác MNPQ để chu vi tứ giác MNPQ nhỏ nhất
3/ Lấy I nằm trong tam giác ABC nhọn. Vẽ \(IH⊥BC,IK⊥AC,IL⊥AB\). Xác định vị trí của I để \(AL^2+BH^2+CK^2\) nhỏ nhất
4/ Cho tam giác ABC nhọn. Tìm điểm M trong tam giác sao cho AM.BC+BM.AC+CM.AB nhỏ nhất