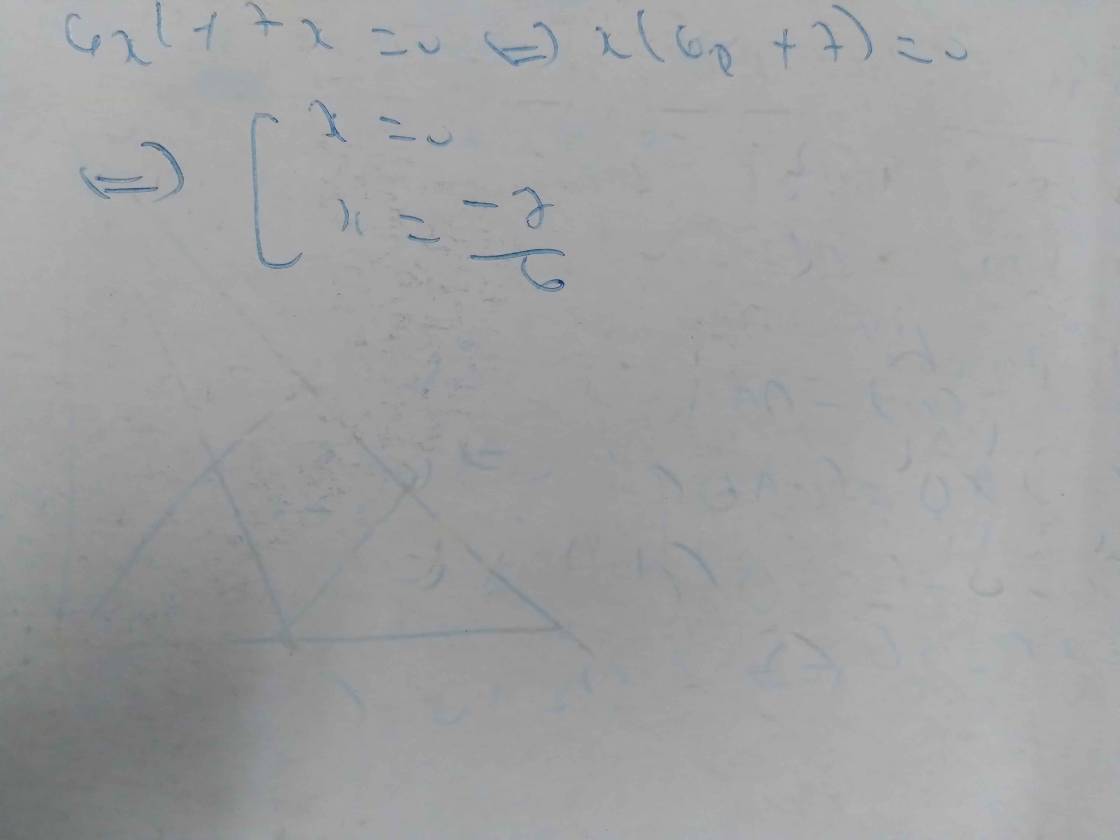Ta có:

      2x^2+7x-9=0

<=>2x^2-2x+9x-9=0

<=>2x(x-1)+9(x-1)=0

<=>(x-1)(2x+9)=0

<=>x-1=0 hoặc 2x+9=0

+)x-1=0<=>x=1

+)2x+9=0<=>2x=-9<=>x=-9/2

Học tốt

Ta có:
\(4x^2+\dfrac{2}{5}x\)
\(=x\left(4x+\dfrac{2}{5}\right)\)
Do đó để đa thức \(4x^2+\dfrac{2}{5}x\) có nghiệm thì \(x\left(4x+\dfrac{2}{5}\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\4x+\dfrac{2}{5}=0\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\4x=-\dfrac{2}{5}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=-\dfrac{1}{10}\end{matrix}\right.\)
Vậy nghiệm của đa thức là \(x\in\left\{0;-\dfrac{1}{10}\right\}\)

=>2x(2x+1/5)=0

=>x=0 hoặc x=-1/10

Đặt f(x) = 2x² + 7x - 9

f(x) = 0 <=> 2x² + 7x - 9 = 0 

            <=> ( x - 1 )( 2x + 9 ) = 0

            <=> x - 1 = 0 hoặc 2x + 9 = 0

            <=> x = 1 hoặc x = -9/2

Vậy nghiệm của đa thức là 1 và -9/2

\(2x^2+7x-9=0\)

\(x\left(2x+7-9\right)=0\)

\(\Rightarrow\orbr{\begin{cases}x=0\\2x+7-9=0\end{cases}\Rightarrow\orbr{\begin{cases}x=0\\2x=2\end{cases}\Rightarrow}\orbr{\begin{cases}x=0\\x=1\end{cases}}}\)

Vậy đa thức có 2 nghiệm là x=0 và x=1

\(\Leftrightarrow2x^2+7x-9=0\)

\(\Leftrightarrow2x^2+7x=9\)

\(\Leftrightarrow2x.x+7x=9\)

\(\Leftrightarrow x\left(2x+7\right)=9\)

\(th1\orbr{\begin{cases}x=1\\2x+7=9\end{cases}\Leftrightarrow x=1}\)

\(th2\orbr{\begin{cases}x=9\\2x+7=1\end{cases}\Leftrightarrow\orbr{\begin{cases}x=9\\x=-3\end{cases}}}\)

\(th3\orbr{\begin{cases}x=-1\\2x+7=-9\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-1\\x=-8\end{cases}}}\)

\(th4\orbr{\begin{cases}x=-9\\2x+7=-1\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-9\\x=-4\end{cases}}}\)

\(th5\orbr{\begin{cases}x=3\\2x+7=3\end{cases}\Leftrightarrow\orbr{\begin{cases}x=3\\x=-4\end{cases}}}\)

\(th5\orbr{\begin{cases}x=-3\\2x+7=-3\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-3\\x=-5\end{cases}}}\)

vậy nghiệm của đa thức là \(\pm1;\pm3;-4;-5\)

Phân tích đa thức thành nhân tử thôi bạn :

Ta có :

\(h\left(x\right)=x^2+5x+6\)

\(h\left(x\right)=x\left(x+2\right)+3\left(x+2\right)\)

\(h\left(x\right)=\left(x+2\right)\left(x+3\right)\)

\(\Rightarrow N_oh\left(x\right)=-2;-3\)

\(g\left(x\right)=2x^2+7x-9\)

\(g\left(x\right)=2x^2+9x-2x-9\)

\(g\left(x\right)=2x\left(x-1\right)+9\left(x-1\right)\)

\(g\left(x\right)=\left(x-1\right)\left(2x+9\right)\)

\(\Rightarrow N_og\left(x\right)=1;-4,5\)

ko biet

haha

a, 4x^3 +3x^2+7x

b, = 0

a) \(f\left(x\right)=x^2+7x-8=0\)

\(\Leftrightarrow f\left(x\right)=x^2-x+8x-8=0\)

​\(\Leftrightarrow f\left(x\right)=\left(x^2-x\right)+\left(8x-8\right)=0\)​

\(\Leftrightarrow f\left(x\right)=x\left(x-1\right)+8\left(x-1\right)=0\)

\(\Leftrightarrow f\left(x\right)=\left(x-1\right)\left(x+8\right)=0\)

\(\Rightarrow x-1=0\) hoặc  \(x+8=0\)

Nếu \(x-1=0\Rightarrow x=1\) 

Nếu  \(x+8=0\Rightarrow x=-8\)

Vậy đa thức f(x) có nghiệm là 1 và -8

b) \(k\left(x\right)=5x^2+9x+4=0\)

\(\Leftrightarrow k\left(x\right)=5x^2+5x+4x+4=0\)

\(\Leftrightarrow k\left(x\right)=\left(5x^2+5x\right)+\left(4x+4\right)=0\)

\(\Leftrightarrow k\left(x\right)=5x\left(x+1\right)+4\left(x+1\right)=0\)

\(\Leftrightarrow k\left(x\right)=\left(x+1\right)\left(5x+4\right)=0\)

\(\Rightarrow x+1=0\) hoặc \(5x+4=0\)

Nếu \(x+1=0\Rightarrow x=-1\)

Nếu \(5x+4=0\Rightarrow x=-\frac{4}{5}\)

Vậy đa thức k(x) có nghiệm là -1 và -4/5

Đặt `6x^2+7x=0`

`-> 6x*x+7x=0`

`-> x(6x+7)=0`

`->`\(\left[{}\begin{matrix}x=0\\6x+7=0\end{matrix}\right.\)

`->`\(\left[{}\begin{matrix}x=0\\6x=0-7\end{matrix}\right.\)

`->`\(\left[{}\begin{matrix}x=0\\6x=-7\end{matrix}\right.\)

`->`\(\left[{}\begin{matrix}x=0\\x=-\dfrac{7}{6}\end{matrix}\right.\)

Vậy, nghiệm của đa thức là `x=0, x=-7/6`.

`@`\(\text{dn inactive.}\)