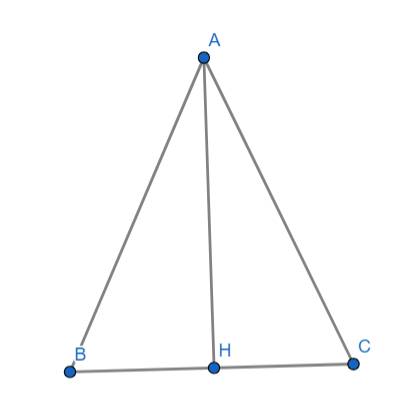
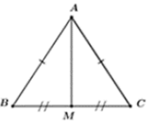
Cho ΔABC cân tại a, có AB = 5cm; BC=6cm, tia phân giác AD của \(\widehat{BAC}\) cắt đường trung tuyến BE của tam giác tại G. Tia CG cắt AB tại F.
a. So sánh số đo của \(\widehat{ABC}\) và \(\widehat{BAC}\)
b. ΔABD = ΔACD
c. C/m F là trung điểm của AB
d. Tính độ dài BG