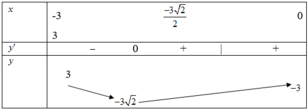
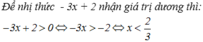tìm tất cả các số dương x để x2 là bội của 3x - 2

Những câu hỏi liên quan
Tìm tất cả các số tự nhiên để 2^n - 1 là bội của 5
CM: nếu x, y thuộc N và x + 2y là bội của 5 thì 3x - 4y cũng là bội của 5
Tìm tất cả các số nguyên dương x để x
2 + 8x là số chính phương.
Bài 1. Tìm tất cả các số nguyên dương x để x2 + 8x là số chính phương.
-Đặt \(x^2+8x=a^2\)
\(\Rightarrow x^2+8x+16=a^2+16\)
\(\Rightarrow\left(x+4\right)^2-a^2=16\)
\(\Rightarrow\left(x+a+4\right)\left(x-a+4\right)=16\)
-Vì \(x,a\) là các số nguyên dương \(\Rightarrow x+a+4>x-a+4\) và \(16=16.1=8.2=4.4\)
\(\Rightarrow x+a+4=16;x-a+4=1\Rightarrow x=\dfrac{9}{2};a=\dfrac{15}{2}\left(loại\right)\)
\(x+a+4=8;x-a+4=2\Rightarrow x=1;a=3\left(nhận\right)\)
\(x+a+4=4;x-a+4=4\Rightarrow x=a=0\left(nhận\right)\)
-Vậy \(x\in\left\{0;1\right\}\)
Đúng 1
Bình luận (0)
Hình bên là đồ thị của hàm số
y
x
3
-
3
x
Tìm tất cả các giá trị thực của tham số m để phương trình
64
|
x
|
3
(
x
2
+
1
)
2
(
12
|
x
|
+
m
(
x
2
+
1
)
)...
Đọc tiếp
Hình bên là đồ thị của hàm số y = x 3 - 3 x Tìm tất cả các giá trị thực của tham số m để phương trình 64 | x | 3 = ( x 2 + 1 ) 2 ( 12 | x | + m ( x 2 + 1 ) ) có nghiệm.
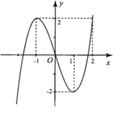
A.![]()
B. Với mọi m
C. ![]()
D. ![]()
Đáp án A
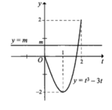
![]() (*)
(*)
Đặt ![]()
Yêu cầu bài toán trở thành: Tìm m để phương trình ![]() có nghiệm
có nghiệm ![]()
Từ đồ thị đã cho, ta suy ra đồ thị của hàm số ![]()
Từ đó ta có kể quả thỏa mãn yêu cầu bài toán ![]()
Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để hệ sau có nghiệm
x
2
-
3
x
+
2
≤
0
m
x...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để hệ sau có nghiệm
x 2 - 3 x + 2 ≤ 0 m x 2 - 2 ( 2 m + 1 ) x + 5 m + 3 ≥ 0
A. m > -1/2
B. m = -1/2
C. m ≥ -1/2
D. không tồn tại
Chọn C
Ta có bất phương trình x2- 3x+ 2≤ 0 khi và chỉ khi 1≤ x≤ 2
Yêu cầu bài toán tương đương với bất phương trình:
mx2-2( 2m+1) x+ 5m+3≤0 (1)
có nghiệm x: 1≤ x≤ 2
+ Ta đi tìm m để bất phương trình (1) vô nghiệm trên S
Tức là bpt f( x) = mx2-2( 2m+1) x+ 5m+3< 0 (2)
đúng với mọi x ∈ S
+ Nếu m= 0 (2) trờ thành: -2x+ 3≤0 hay x> 3/2 nên (2) không đúng với mọi x ∈ S
+ Nếu m≠ 0 tam thức f(x) có hệ số a= m, biệt thức ∆’ = -m2+m+ 1
Bảng xét dấu:


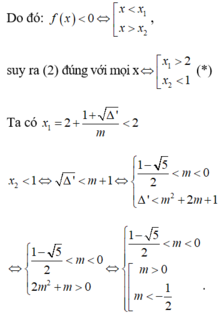
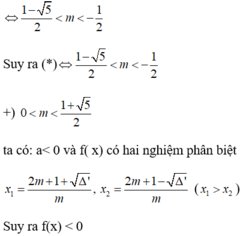

Đúng 0
Bình luận (0)
Tìm tất cả các giá trị của tham số m để phương trình
x
-
m
9
-
x
2
0
có đúng 1 nghiệm dương? A.
m
∈
(
-
3
;
2
]
B.
m
∈
(
-
3
;
2
]
∪
-
3
2...
Đọc tiếp
Tìm tất cả các giá trị của tham số m để phương trình x - m 9 - x 2 = 0 có đúng 1 nghiệm dương?
A. m ∈ ( - 3 ; 2 ]
B. m ∈ ( - 3 ; 2 ] ∪ - 3 2
C. m ∈ 0 ; 3
D. m = ± 3 2
Tìm tất cả các giá trị của x để nhị thức - 3 x + 2 nhận giá trị dương.
A. x < 3 2
B. x < 2 3
C. x < - 3 2
D. x > 2 3
Tìm tất cả các giá trị dương của tham số m để phương trình x2+2(m+1)x-2m-3=0 có hai nghiệm trái dấu x1;x2 thỏa mãn \(\sqrt{2x_2-1}=x_1+22\)
Tìm tất cả các giá trị thực của tham số m để bất phương trình
x
2
+
3
x
+
3
x
+
1
≥
m
nghiệm đúng với mọi
x
∈
0
;
1
A.
m
≥...
Đọc tiếp
Tìm tất cả các giá trị thực của tham số m để bất phương trình x 2 + 3 x + 3 x + 1 ≥ m nghiệm đúng với mọi x ∈ 0 ; 1
A. m ≥ 3
B. m ≤ 7 2
C. m ≥ 7 2
D. m ≤ 3
Đáp án D
Để bất phương trình m ≤ f x = x 2 + 3 x + 3 x + 1 ; ∀ x ∈ 0 ; 1 ⇔ m ≤ min 0 ; 1 f x
Xét hàm số f x = x 2 + 3 x + 3 x + 1 trên 0 ; 1 ⇒ min 0 ; 1 f x = 3 . Vậy m ≤ 3
Đúng 0
Bình luận (0)