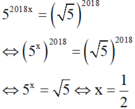so sánh 52018-2016/52018-2017 với 52018-2018/52018-2019

Những câu hỏi liên quan
Tìm nghiệm của phương trình
5
2018
5
2018
. A.
x
1
2
B.
x
1
-
log
5
2
C.
x
2
D.
x...
Đọc tiếp
Tìm nghiệm của phương trình 5 2018 = 5 2018 .
A. x = 1 2
B. x = 1 - log 5 2
C. x = 2
D. x = - log 5 2
Tìm nghiệm của phương trình
5
2018
x
5
2018
.
A.
x
1
2
B.
x
1
−
log
5
2
C.
x
2
D.
x
−
log
5
2
Đọc tiếp
Tìm nghiệm của phương trình 5 2018 x = 5 2018 .
A. x = 1 2
B. x = 1 − log 5 2
C. x = 2
D. x = − log 5 2
Đáp án A
Ta có:
5 2018 x = 5 2018 ⇔ 5 x 2018 = 5 2018 ⇔ 5 x = 5 ⇔ x = 1 2
Đúng 0
Bình luận (0)
Tìm nghiệm của phương trình
5
2018
x
5
2018
.
A.
x
1
2
B.
x
1
−
log
5
2
C. x 2 D.
x
−
log
5
2
Đọc tiếp
Tìm nghiệm của phương trình 5 2018 x = 5 2018 .
A. x = 1 2
B. x = 1 − log 5 2
C. x = 2
D. x = − log 5 2
Gọi x là số các chữ số của số 2 2018 , y là số các chữ số của số 5 2018 . Tính tổng x+y
Ta thấy số 2 2018 có x chữ số
Mà số nhỏ nhất có x chữ số là 10 x - 1
số nhỏ nhất có x+1 chữ số là 10 x
=> 10 x - 1 < 2 2018 < 10 x
Tương tự có 10 y - 1 < 5 2018 < 10 y
Do đó => 10 x - 1 . 10 y - 1 < 2 2018 . 5 2018 < 10 x . 10 y
=> 10 x + y - 2 < 10 2018 < 10 x + y
=> x + y – 2 < 2018 < x + y
Mà x + y ∈ N suy ra x + y = 2019
Đúng 0
Bình luận (0)
Ko dùng máy tính hãy so sánh 2016/2017+2017/2018+2018/2019+2019/2016 với 4
so sánh : P = 2016/2017 + 2017/2018 + 2018/2019 và Q = 2016 + 2017 + 2018/2017 + 2018 + 2019
Ta có :
\(\frac{2016}{2017}>\frac{2016}{2017+2018+2019}\)
\(\frac{2017}{2018}>\frac{2017}{2017+2018+2019}\)
\(\frac{2018}{2019}>\frac{2018}{2017+2018+2019}\)
\(\Rightarrow\frac{2016}{2017}+\frac{2017}{2018}+\frac{2018}{2019}>\) \(\frac{2016}{2017+2018+2019}+\frac{2017}{2017+2018+2019}+\frac{2018}{2017+2018+2019}\)
\(\Rightarrow P>\frac{2016+2017+2018}{2017+2018+2019}\)
\(\Rightarrow P>Q\)
Chúc bạn học tốt !!!
Đúng 0
Bình luận (0)
vì P có các số bé hơn 1 còn Q có các số lớn hơn 1 =>P<Q
Vậy P<Q.
mình làm hơi tắt xin bạn thông cảm bạn tự viết các số có trong P;Q ra nhá
Đúng 0
Bình luận (0)
Đơn giản P < Q
Vì Nhìn sơ qua ta thấy tổng P gồm các phân số bé hơn 1
Tổng Q có 3 phân số lớn hơn 1
Đúng 0
Bình luận (0)
Cho A=2016/2017+2017/2018+2018/2019.
So sánh A với 3
\(A=\frac{2016}{2017}+\frac{2017}{2018}+\frac{2018}{2019}=\left(1-\frac{1}{2017}\right)+\left(1-\frac{1}{2018}\right)+\left(1-\frac{1}{2019}\right)\)
\(A=3-\left(\frac{1}{2017}+\frac{1}{2018}+\frac{1}{2019}\right)< 3\)
Đúng 0
Bình luận (0)
Ta có :
2016/2017 < 1
2017/2018 < 1
2018/2019 < 1
Mà 2016/2017 + 2017/2018 + 2018/2019 < 1 + 1 + 1 = 3
Nên A < 3
Đúng 0
Bình luận (0)
Cho A=2016/2017+2017/2018+2018/2019.
So sánh A với 3.
\(A=\frac{2016}{2017}+\frac{2017}{2018}+\frac{2018}{2019}\)
Ta có:
\(\frac{2016}{2017}< 1\)
\(\frac{2017}{2018}< 1\)
\(\frac{2018}{2019}< 1\)
\(\Rightarrow\frac{2016}{2017}+\frac{2017}{2018}+\frac{2018}{2019}< 1+1+1=3\)
\(\Rightarrow A< 3\)
Vậy \(A< 3\)
Tham khảo nhé
Đúng 0
Bình luận (0)
\(\frac{2016}{2017}+\frac{2017}{2018}+\frac{2018}{2019}\)
\(=1-\frac{1}{2017}+1-\frac{1}{2018}+1-\frac{1}{2019}\)
\(=\left(1+1+1\right)-\left(\frac{1}{2017}+\frac{1}{2018}+\frac{1}{2019}\right)\)
\(=3-\left(\frac{1}{2017}+\frac{1}{2018}+\frac{1}{2019}\right)< 3\)
Vậy \(\frac{2016}{2017}+\frac{2017}{2018}+\frac{2018}{2019}< 3\left(đpcm\right)\)
Đúng 0
Bình luận (0)
vì 2016/2017 < 1
2017/2018 < 1
2018/2019 < 1
Nên A= 2016/2017 + 2017/2018 + 2018/2019 < 1 + 1 + 1 = 3
Vậy A < 3.
Tk nha ♡♡
Đúng 0
Bình luận (0)
So sánh
P= 2016/2017+2017/2018+2018/2019 và
Q= 2+2016+2017+2018/2017+2018+2019
Ghi đầy đủ các bước hộ mk nha
#)Giải :
\(Q=2+\frac{2016}{2017+2018+2019}+\frac{2017}{2017+2018+2019}+\frac{2018}{2017+2018+2019}\)
Ta thấy : \(2>\frac{2016}{2017};2>\frac{2017}{2018};2>\frac{2018}{2019}\left(1\right)\)
\(\frac{2016}{2017+2018+2019}< \frac{2016}{2017}\left(2\right)\)
\(\frac{2017}{2017+2018+2019}< \frac{2017}{2018}\left(3\right)\)
\(\frac{2018}{2017+2018+2019}< \frac{2018}{2019}\left(4\right)\)
Từ (1) (2) (3) (4) \(\Rightarrow P>Q\)
Đúng 0
Bình luận (0)
so sánh a và b biết a=2016/2017+2017/2018+2018/2019+2019/2016 và b=1/8+1/9+1/10+...+1/63