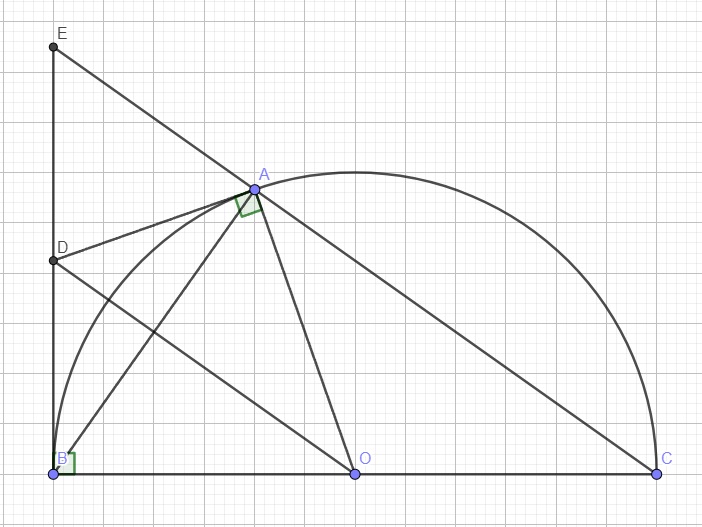
Bài 4. (4 điểm) Cho nửa đường tròn (O; R) đường kính BC. Lấy điểm A trên tia đối của tia CB. Kẻ tiếp tuyến AF của nửa đường tròn (O) (với F là tiếp điểm), tia AF cắt tiếp tuyến Bx của nửa đường tròn tại D. Biết AF = 4R/3. a) Chứng minh tứ giác OBDF nội tiếp. Định tâm I đường tròn ngoại tiếp tứ giác OBDF. b) Tính Cos góc DAB. c) Kẻ OM ⊥ BC (M ∈ AD). Chứng minh BD/DM - DM/AM = 1. d) Tính diện tích phần hình tứ giác OBDM ở bên ngoài nửa đường tròn (O) theo R.

Những câu hỏi liên quan
Bài 4: Cho nửa đường tròn (O;R) đường kính BC. Trên nửa mặt phẳng bờ BC chứa nửa đường trònvẽ tiếp tuyến Bx của(O), A là điểm bất kì thuộc nửa đường tròn sao cho AB Tiếp tuyến tại 4 của (O) cắt tia Bx tại D.a) Chứng minh bốn điểm A,D,B,O cùng thuộc một đường tròn;AB tại điểmK.b) Tia CA cắt Bx tại E. Chứng minh rằng ODsong song CEvà CA.CE4R;
Đọc tiếp
Bài 4: Cho nửa đường tròn (O;R) đường kính BC. Trên nửa mặt phẳng bờ BC chứa nửa đường tròn
vẽ tiếp tuyến Bx của(O), A là điểm bất kì thuộc nửa đường tròn sao cho AB Tiếp tuyến tại 4 của (O) cắt tia Bx tại D.
a) Chứng minh bốn điểm A,D,B,O cùng thuộc một đường tròn;
AB tại điểm
K.
b) Tia CA cắt Bx tại E. Chứng minh rằng OD
song song CE
và CA.CE=4R;
a.
Do AD là tiếp tuyến tại A \(\Rightarrow\widehat{OAD}=90^0\)
\(\Rightarrow\) 3 điểm O, A, D thuộc đường tròn đường kính OD (1)
BD là tiếp tuyến tại B \(\Rightarrow\widehat{OBD}=90^0\)
\(\Rightarrow\) 3 điểm O, B, D thuộc đường tròn đường kính OD (2)
(1);(2) \(\Rightarrow\) 4 điểm A, D, B, O cùng thuộc đường tròn đường kính OD
b.
Do D là giao điểm 2 tiếp tuyến tại A và B, theo t/c hai tiếp tuyến cắt nhau
\(\Rightarrow DA=DB\)
Mà \(OA=OB=R\)
\(\Rightarrow OD\) là trung trực của AB \(\Rightarrow OD\perp AB\) (3)
BC là đường kính và A thuộc đường tròn nên \(\widehat{BAC}\) là góc nt chắn nửa đường tròn
\(\Rightarrow\widehat{BAC}=90^0\Rightarrow BA\perp CA\) (4)
(3);(4) \(\Rightarrow OD||CA\) (cùng vuông góc AB) hay \(OD||CE\)
Áp dụng hệ thức lượng trong tam giác vuông BCE với đường cao BA ứng với cạnh huyền:
\(BC^2=CA.CE\Rightarrow\left(2R\right)^2=CA.CE\)
\(\Rightarrow CA.CE=4R^2\)
Đúng 1
Bình luận (2)
Em kiểm tra lại đề bài, đoạn này là sao nhỉ: "Tiếp tuyến tại 4 của (O) "
Đúng 0
Bình luận (4)
đề bài: Cho nửa đường tròn (O,R), AB đường kính.Trên nửa mặt phẳng bờ AB chứa nửa đường tròn, kẻ tiếp tuyến Bx với (O).Điểm M di động trên tia Bx, AM cắt (O) tại N(N#A). Gọi E là trung điểm đoạn AN.CMR: 4 điểm E,O,B,M cùng thuộc 1 đường tròn. Em xin cảm ơn các thầy cô và mong các thầy cô có thể chỉ cho em cách vẽ hình bài này và phương pháp làm bài cm 4 điểm cùng thuộc 1 đường tròn ạ(Em mới học hết chương 2 đường tròn lớp 9 ạ!)
Đọc tiếp
đề bài: Cho nửa đường tròn (O,R), AB đường kính.Trên nửa mặt phẳng bờ AB chứa nửa đường tròn, kẻ tiếp tuyến Bx với (O).Điểm M di động trên tia Bx, AM cắt (O) tại N(N#A). Gọi E là trung điểm đoạn AN.
CMR: 4 điểm E,O,B,M cùng thuộc 1 đường tròn. Em xin cảm ơn các thầy cô và mong các thầy cô có thể chỉ cho em cách vẽ hình bài này và phương pháp làm bài cm 4 điểm cùng thuộc 1 đường tròn ạ(Em mới học hết chương 2 đường tròn lớp 9 ạ!)
Bài 4: Cho nửa đường tròn (O;R) đường kính BC. Trên nửa mặt phẳng bờ BC chứa nửa đường trònvẽ tiếp tuyến Bx của(O), A là điểm bất kì thuộc nửa đường tròn sao cho AB Tiếp tuyến tại A của (O) cắt tia Bx tại D.a) Chứng minh bốn điểm A,D,B,O cùng thuộc một đường tròn;AB tại điểmK.b) Tia CA cắt Bx tại E. Chứng minh rằng ODsong song CEvà CA.CE4R;
Đọc tiếp
Bài 4: Cho nửa đường tròn (O;R) đường kính BC. Trên nửa mặt phẳng bờ BC chứa nửa đường tròn
vẽ tiếp tuyến Bx của(O), A là điểm bất kì thuộc nửa đường tròn sao cho AB Tiếp tuyến tại A của (O) cắt tia Bx tại D.
a) Chứng minh bốn điểm A,D,B,O cùng thuộc một đường tròn;
AB tại điểm
K.
b) Tia CA cắt Bx tại E. Chứng minh rằng OD
song song CE
và CA.CE=4R;
a: Xét tứ giác ADBO có
\(\widehat{DBO}+\widehat{DAO}=90^0+90^0=180^0\)
=>ADBO là tứ giác nội tiếp
=>A,D,B,O cùng thuộc một đường tròn
b: Xét (O) có
ΔBAC nội tiếp
BC là đường kính
Do đó: ΔBAC vuông tại A
=>BA\(\perp\)AC tại A
=>BA\(\perp\)CE tại A
Xét (O) có
DA,DB là các tiếp tuyến
DO đó: DA=DB
=>D nằm trên đường trung trực của AB(1)
ta có: OA=OB
=>O nằm trên đường trung trực của AB(2)
Từ (1),(2) suy ra OD là đường trung trực của AB
=>OD\(\perp\)AB
Ta có: OD\(\perp\)AB
CE\(\perp\)AB
Do đó: OD//CE
Xét ΔEBC vuông tại B có BA là đường cao
nên \(CA\cdot CE=CB^2\)
=>\(CA\cdot CE=\left(2R\right)^2=4R^2\)
Đúng 1
Bình luận (0)
Bài 4: Cho nửa đường tròn (O; R) đường kính AB. Điểm C di động trên nửa đường tròn (C khác A, B), gọi M là điểm chính giữa cung AC, BM cắt AC tại H và cắt tia tiếp tuyến Ax của nửa đường tròn (O) tại K, AM cắt BC tại D. a) Chứng minh tứ giác DMHC nội tiếp và HM. HB HA.HC b) Chứng minh ABD cân đỉnh B c) Chứng minh KD là tiếp tuyến của (B; BA). d) Tứ giác AKDH là hình gì? Vì sao? e) Đường tròn ngoại tiếp BHD cắt đường tròn (B; BA) tại N. Chứng minh A, C, N thẳng hàng.
Đọc tiếp
Bài 4: Cho nửa đường tròn (O; R) đường kính AB. Điểm C di động trên nửa đường tròn (C khác A, B), gọi M là điểm chính giữa cung AC, BM cắt AC tại H và cắt tia tiếp tuyến Ax của nửa đường tròn (O) tại K, AM cắt BC tại D. a) Chứng minh tứ giác DMHC nội tiếp và HM. HB = HA.HC b) Chứng minh ABD cân đỉnh B c) Chứng minh KD là tiếp tuyến của (B; BA). d) Tứ giác AKDH là hình gì? Vì sao? e) Đường tròn ngoại tiếp BHD cắt đường tròn (B; BA) tại N. Chứng minh A, C, N thẳng hàng.
a: góc AMB=góc ACB=90 độ
=>BM vuông góc DA và AC vuông góc DB
góc DMH+góc DCH=90+90=180 độ
=>DMHC nội tiếp
Xét ΔHMA vuông tại M và ΔHCB vuông tại C có
góc MHA=góc CHB
=>ΔHMA đồng dạng với ΔHCB
=>HM/HC=HA/HB
=>HM*HB=HA*HC
b: góc DBM=góc CBM=1/2*sđ cung CM
góc MBA=1/2*sđ cung MA
mà sđ cung CM=sđ cung MA
nên góc DBM=góc ABM
=>BM là phân giác của góc DBA
Xét ΔBDA có
BM vừa là đường cao, vừa là phân giác
=>ΔBDA cân tại B
d: Xét ΔMAK vuông tại M và ΔMDH vuông tại M có
MA=MD
góc MAK=góc MDH
=>ΔMAK=ΔMDH
=>MK=MH
Xét tứ giác AKDH có
M là trung điểm chung của AD và KH
AD vuông góc KH
=>AKDH là hình thoi
Đúng 0
Bình luận (0)
Bài 4. (2đ): Cho nửa đường tròn tâm O đường kính AB 2R. Từ A và B lần lượt kẻ hai tiếp tuyến Ax và By với nửa đường tròn. Qua điểm M thuộc nửa đường tròn (M khác A và B) kẻ tiếp tuyến thứ ba cắt các tiếp tuyến Ax và By lần lượt tại C và D. a. Chứng minh rằng :Tứ giác AOMC nội tiếp. b. KhiBAM 600. Chứng tỏ BDM là tam giác đều và tính diện tích của hình quạt tròn chắn cung MB của nửa đường tròn đã cho theo R.
Đọc tiếp
Bài 4. (2đ): Cho nửa đường tròn tâm O đường kính AB = 2R. Từ A và B lần lượt kẻ hai tiếp tuyến
Ax và By với nửa đường tròn. Qua điểm M thuộc nửa đường tròn (M khác A và B) kẻ tiếp
tuyến thứ ba cắt các tiếp tuyến Ax và By lần lượt tại C và D.
a. Chứng minh rằng :Tứ giác AOMC nội tiếp.
b. KhiBAM= 600. Chứng tỏ BDM là tam giác đều và tính diện tích của hình quạt tròn
chắn cung MB của nửa đường tròn đã cho theo R.
a: góc OAC+góc OMC=180 độ
=>OACM nội tiếp
b: góc BOM=2*60=120 độ
=>góc BDM=60 độ
=>ΔBMD đều
\(S_{qMB}=\dfrac{pi\cdot R^2\cdot120}{360}=\dfrac{1}{3}\cdot pi\cdot R^2\)
Đúng 0
Bình luận (1)
Bài 5: Cho nửa đường tròn tâm O, đường kính AB. Vẽ 2 tiếp tuyến Ax, By của nửa (O). Gọi C là điểm trên nửa (O) sao cho AC > BC. Tiếp tuyến tại C của nửa (O) cắt Ax và By lần lượt ở D và E.
a) Cm ∆ABC vuông và AD + BE = ED.
b) Cm 4 điểm A, D, C, O cùng thuộc 1 đường tròn và góc ADO = góc CAB.
c) DB cắt nửa (O) tại F và cắt AE tại I. Tia CI cắt AB tại K. Cm IC = IK.
a: Xét (O) có
ΔACB nội tiếp
AB là đường kính
Do đó:ΔACB vuông tại C
Xét (O) có
DC,DA là tiếp tuyến
Do đó: DC=DA
Xét (O)có
EC,EB là tiếp tuyến
Do đó: EC=EB
DC+CE=DE
mà DC=DA và EC=EB
nên DA+EB=DE
b: Xét tứ giác DAOC có \(\widehat{DAO}+\widehat{DCO}=90^0+90^0=180^0\)
=>DAOC là tứ giác nội tiếp
=>D,A,O,C cùng thuộc một đường tròn
Xét ΔOAC có OA=OC=R
nên ΔOAC cân tại O
ADCO là tứ giác nội tiếp
=>\(\widehat{ADO}=\widehat{ACO}\)
mà \(\widehat{ACO}=\widehat{OAC}\)(ΔOAC cân tại O)
nên \(\widehat{ADO}=\widehat{OAC}=\widehat{CAB}\)
Đúng 3
Bình luận (0)
Bài 4: Cho nửa đường tròn (O; R) đường kính AB, kẻ hai tiếp tuyến Ax, By. Từ M thuộc nửa đường tròn kẻ tiếp tuyển thứ ba cắt Ax, By lần lượt tại C và D. a/ Tính số đo góc COD b/C/m: AC.BD không đổi khi điểm M di chuyển trên nửa đường tròn. c/Gọi N là giao điểm của BC và AD. C/m: MN // AC.
a: Xét (O) có
CM,CA là các tiếp tuyến
Do đó: OC là phân giác của góc MOA
=>\(\widehat{MOA}=2\cdot\widehat{MOC}\)
Xét (O) có
DM,DB là các tiếp tuyến
Do đó: OD là phân giác của góc MOB
=>\(\widehat{MOB}=2\cdot\widehat{MOD}\)
Ta có: \(\widehat{MOA}+\widehat{MOB}=180^0\)(hai góc kề bù)
=>\(2\cdot\left(\widehat{MOD}+\widehat{MOC}\right)=180^0\)
=>\(2\cdot\widehat{COD}=180^0\)
=>\(\widehat{COD}=90^0\)
b: Xét (O) có
CM,CA là các tiếp tuyến
Do đó: CM=CA
Xét (O) có
DM,DB là các tiếp tuyến
Do đó: DM=DB
Xét ΔCOD vuông tại O có OM là đường cao
nên \(MC\cdot MD=OM^2\)
mà MC=CA và DM=DB
nên \(AC\cdot DB=OM^2=R^2\) không đổi khi M di chuyển trên (O)
c: Xét ΔNAC và ΔNDB có
\(\widehat{NAC}=\widehat{NDB}\)(hai góc so le trong, AC//DB)
\(\widehat{ANC}=\widehat{DNB}\)(hai góc đối đỉnh)
Do đó: ΔNAC đồng dạng với ΔNDB
=>\(\dfrac{NA}{ND}=\dfrac{NC}{NB}=\dfrac{AC}{DB}=\dfrac{CM}{MD}\)
Xét ΔDCA có \(\dfrac{DM}{MC}=\dfrac{DN}{NA}\)
nên MN//AC
Đúng 0
Bình luận (0)
2) Cho điểm M thuộc nửa đường tròn (O; R) đường kính AB. Trên nửa mặt phẳng bờ AB chứa điểm M, kẻ các tia tiếp tuyến Ax, By với nửa đường tròn. Tiếp tuyến tại M của nửa đường tròn cắt tia Ax tại C.a) Chứng minh rằng 4 điểm A, C, O, M cùng thuộc một đường tròn. Chỉ rõ tâm đường đó.b) Tiếp tuyến tại M cắt tia By tại D. Chứng minh rằng AC + BD CD và ACOD vuông tại O.c) Gọi E là giao điểm của AD và BC, K là giao điểm của ME và AB. Chứng minh rằng E là trung điểm MK.
Đọc tiếp
2) Cho điểm M thuộc nửa đường tròn (O; R) đường kính AB. Trên nửa mặt phẳng bờ AB chứa điểm M, kẻ các tia tiếp tuyến Ax, By với nửa đường tròn. Tiếp tuyến tại M của nửa đường tròn cắt tia Ax tại C.
a) Chứng minh rằng 4 điểm A, C, O, M cùng thuộc một đường tròn. Chỉ rõ tâm đường đó.
b) Tiếp tuyến tại M cắt tia By tại D. Chứng minh rằng AC + BD = CD và ACOD vuông tại O.
c) Gọi E là giao điểm của AD và BC, K là giao điểm của ME và AB. Chứng minh rằng E là trung điểm MK.
a: Xét tứ giác CAOM có góc CAO+góc CMO=180 độ
nên CAOM là tứ giác nội tiếp
Tâm là trung điểm của OC
b: Xét (O) có
CM,CA là các tiếp tuyến
nên CM=CA và OC là phân giác của góc MOA(1)
Xét (O) có
DM,DB là các tiếp tuyến
nên DM=DB và OD là phân giác của góc MOB(2)
Từ (1), (2) suy ra góc COD=1/2*180=90 độ
AC+BD=CM+MD=CD
Đúng 0
Bình luận (0)
Câu 4 (3,5 điểm) Cho nửa đường tròn tâm O, đường kính BC, 4 là điểm chính giữa cung BC. Dung hình bình hành ABCD. Gọi H là chân đường cao kẻ từ 4 xuống BD, E là giao điểm của BD với nửa đường tròn (O). a. Chứng minh tứ giác AHCD nội tiếp. b. Chứng minh 4OE = 2CAH c. Chứng minh DE.DB = 2.4C2