Trên đường tròn ( O; R ) lấy 10 điểm phân biệt :
a) Hỏi qua 10 điểm đó vẽ được tất cả bao nhiêu dây ? Bao nhiêu cung?
b) Trên hình vẽ có tất cả bao nhiêu góc?
c) Cũng hỏi như trên với n điểm trên đường tròn
Những câu hỏi liên quan
Cho đường tròn (O) và điểm A cố định trên đường tròn. Điểm B chuyển động trên đường tròn. Đường tròn (O’) có vị trí tương đối nào với đường tròn (O) ?
Đường tròn (O’) tiếp xúc trong với đường tròn (O).
Đúng 0
Bình luận (0)
Câu 59: Trên hình bên, ta có đường tròn (O; R)A. Điểm O cách mọi điểm trên đường tròn một khoảng RB. Điểm O cách mọi điểm trên hình tròn một khoảng R O R C. Điểm O nằm trên đường tròn D. Chỉ có câu C đúngCâu 60: Gọi S1 là diện tích hình tròn bán kính R1 1 cmS2 là diện tích hình tròn bán kính R2 gấp 2 lần bán kính R1. Ta có:A. S2 2S1 B. S2 S1 C. S2 4S1 ...
Đọc tiếp
Câu 59: Trên hình bên, ta có đường tròn (O; R)
A. Điểm O cách mọi điểm trên đường tròn một khoảng R
B. Điểm O cách mọi điểm trên hình tròn một khoảng R
C. Điểm O nằm trên đường tròn
D. Chỉ có câu C đúng
Câu 60: Gọi S1 là diện tích hình tròn bán kính R1 = 1 cm
S2 là diện tích hình tròn bán kính R2 gấp 2 lần bán kính R1. Ta có:
A. S2 = 2S1 B. S2 = S1 C. S2 = 4S1 D. S2 = 3S1
Cho đường tròn (O) và điểm A cố định trên đường tròn. Điểm B chuyển động trên đường tròn
a) Chứng minh rằng trung điểm M của AB chuyển động trên một đường tròn (O') ?
b) Đường tròn (O') có vị trí tương đối nào đối với đường tròn (O) ?
a: \(\widehat{AMO}=90^0\)
nên điểm M chuyển động trên đường tròn đường kính AO
b: Đường tròn (O') tiếp xúc trong với đường tròn (O)
Đúng 0
Bình luận (0)
Cho hai điểm phân biệt B và C cố định trên đường tròn tâm O bán kính O, điểm A di động trên đường tròn O. CMR khi A di động trên đường tròn O thì trực tâm của tam giác ABO di động trên một đường tròn.
Cho đường tròn (O) và 1 điểm P nằm bên trong đường tròn (P khác O). Gọi Q là 1 điểm tùy ý trên đường tròn (O). CMR khi điểm Q chuyển động trên đường tròn (O) thì giao điểm M các đường thẳng kẻ qua O vuông góc với PQ và tiếp tuyến kẻ từ Q của đường tròn (O) chạy trên 1 đường thẳng cố định
Cho đường tròn (O) và 1 điểm P nằm bên trong đường tròn (P khác O). Gọi Q là 1 điểm tùy ý trên đường tròn (O). CMR khi điểm Q chuyển động trên đường tròn (O) thì giao điểm M các đường thẳng kẻ qua O vuông góc với PQ và tiếp tuyến kẻ từ Q của đường tròn (O) chạy trên 1 đường thẳng cố định.
chiu
moi hoc lop 5 thui
doi toan lop 9 o dau ra
Đúng 0
Bình luận (0)
Cho đường tròn (O) và điểm A cố định trên đường tròn. Điểm B chuyển động trên đường tròn. Chứng minh rằng trung điểm M của AB chuyển động trên một đường tròn (O’).
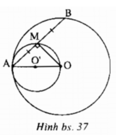
∠ (AMO) = 90 ° . Điểm M chuyển động trên đường tròn (O’) đường kính AO.
Đúng 0
Bình luận (0)
.a)Vẽ đường tròn (O;2cm)
b)Lấy điểm A bất kì trên đường tròn(O;2cm) vẽ đường tròn (A;2cm) đường tròn nay cắt đường tròn tâm O ở trên 2 điểm C,D
c)Vẽ đường tròn (C;2cm)
d)Chứng tỏ rằng đường tròn (C;2cm) đi qua 2 điểm O,A
Cho đường tròn (O), bán kính R 6 cm và một điểm A cách O một khoảng 10 cm. Từ A vẽ tiếp tuyến AB (B là tiếp điểm) với đường tròn (O). Lấy điểm C trên đường tròn (O), tia AC cắt đường tròn (O) tại điểm thứ hai là D. Gọi I là trung điểm của CD. a)Tính độ dài đoạn AB.b)Khi C di chuyển trên đường tròn (O) thì I di chuyển trên đường nào?c) Chứng mimh rằng tích AC.AD không đổi khi C thay đổi trên đường tròn (O).
Đọc tiếp
Cho đường tròn (O), bán kính R = 6 cm và một điểm A cách O một khoảng 10 cm. Từ A vẽ tiếp tuyến AB (B là tiếp điểm) với đường tròn (O). Lấy điểm C trên đường tròn (O), tia AC cắt đường tròn (O) tại điểm thứ hai là D. Gọi I là trung điểm của CD. a)Tính độ dài đoạn AB.
b)Khi C di chuyển trên đường tròn (O) thì I di chuyển trên đường nào?
c) Chứng mimh rằng tích AC.AD không đổi khi C thay đổi trên đường tròn (O).
Mình nói sơ qua nhá:
a) Ta có ΔABO là Δ vuông tại B
Ta tính được AB=8 nhờ vào định lí Py-ta-go
b) Do I là trung điểm của CD nên OI⊥CD, lại suy ra được OI⊥IA
Nên I sẽ chuyển động trên đường tròn đường kính OA (cố định) khi C thay đổi trên đường tròn
c) Chứng minh cho ΔABD∼ΔACB
Suy ra được AC.AD=AB2 không đổi
tk nha bạn
thank you bạn
(^_^)
Đúng 1
Bình luận (1)
Cho 2 đường tròn (O) và (O) cắt nhau tại A và B. Trên nửa mặt phẳng bờ là OO có chứa điểm A dựng tiếp tuyến CD chung của 2 đường tròn (C nằm trên đường tròn (O), D nằm trên đường tròn (O)). Dựng cát tuyến EBF song song với CD (E nằm trên đường tròn (O), F nằm trên đường tròn (O)). Kéo dài EC và FD cắt nhau tại điểm I.Gọi M và N lần lượt là giao điểm của AC và AD với EF. CMR: Tam giác MIN cân.
Đọc tiếp
Cho 2 đường tròn (O) và (O') cắt nhau tại A và B. Trên nửa mặt phẳng bờ là OO' có chứa điểm A dựng tiếp tuyến CD chung của 2 đường tròn (C nằm trên đường tròn (O), D nằm trên đường tròn (O')). Dựng cát tuyến EBF song song với CD (E nằm trên đường tròn (O), F nằm trên đường tròn (O')). Kéo dài EC và FD cắt nhau tại điểm I.Gọi M và N lần lượt là giao điểm của AC và AD với EF. CMR: Tam giác MIN cân.