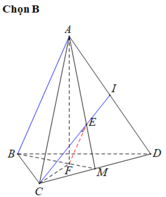
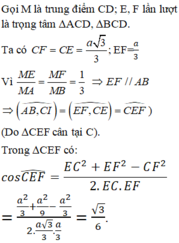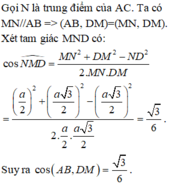cho tứ diện đều abcd . tính cosin giữa AB và CI vs I là trung điểm của AD

Những câu hỏi liên quan
Cho tứ diện đều ABCD cạnh a. Tính cosin góc giữa hai đường thẳng AB và CI với I là trung điểm của AD
A. 3 2
B. 3 6
C. 3 4
D. 1 2
cho tứ diện đều abcd . tính cosin giữa AB và CI vs I là trung điểm của AD
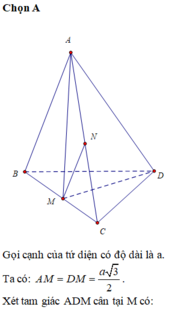
Cho tứ diện đều ABCD, M là trung điểm BC. Tính cosin của góc giữa hai đường thẳng AB và DM
A. 3 6
B. 2 2
C. 3 2
D. 1 2
Cho tứ diện đều ABCD, M là trung điểm BC. Tính cosin của góc giữa hai đường thẳng AB và DM?
A. 3 6
B. 2 2
C. 3 2
D. 1 2
Đáp án A
Giả sử tứ diện đều cạnh a
Gọi H là tâm đường tròn ngoại tiếp Δ B C D ⇒ A H ⊥ B C D
Gọi E là trung điểm
A C ⇒ M E // A B ⇒ A B , D M = M E , M D
Ta có M E = a 2 , E D = M D = a 3 2
cos
A
B
,
D
M
=
cos
M
E
,
M
D
=
cos
E
M
D
⏜
cos
E
M
D
⏜
=
M
E
2
+
M
D
2
−
E
D
2
2
M
E
.
M
D
=
3
6
Đúng 0
Bình luận (0)
Cho tứ diện đều ABCD cạnh a. Tính góc giữa hai đường thẳng CI và AC, với I là trung điểm của AB? A. 100 B. 300 C. 1500 D. 1700
Đọc tiếp
Cho tứ diện đều ABCD cạnh a. Tính góc giữa hai đường thẳng CI và AC, với I là trung điểm của AB?
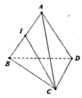
A. 100
B. 300
C. 1500
D. 1700
1.Cho tứ diện đều ABCD cạnh bằng a, gỏi I là trung điểm cạnh AD. Tính góc giữa hai đường thẳng AB và CI.
Cho tứ diện đều ABCD , M là trung điểm của AB . Góc giữa hai đường thẳng CM và DM có cosin bằng:
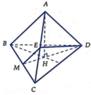
Gọi cạnh của tứ diện là a \(\Rightarrow\) tất cả các mặt bên đều là tam giác đều cạnh a
\(\Rightarrow CM=DM=\frac{a\sqrt{3}}{2}\) (trung tuyến tam giác đều)
\(\Rightarrow cos\widehat{CMD}=\frac{CM^2+DM^2-CD^2}{2CM.DM}=\frac{\frac{3a^2}{4}+\frac{3a^2}{4}-a^2}{2.\frac{3a^2}{4}}=\frac{1}{3}\)
Cho hình chóp SABCD có đáy là hình vuông cạnh a, mặt bên SAB là tam giác đều, vuông góc vs (ABCD) và SC =a căn 2 , Gọi H và K lần lượt là trung điểm của AB và AD. cosin góc giữa SC và (SHD) là?
Cho tứ diện đều ABCD, M là trung điểm của BC. Khi đó cosin của góc giữa hai đường thẳng nào sau đây có giá trị bằng
3
6
A. (AB, DM). B. (AD, DM). C. (AM, DM). D. (AB, AM).
Đọc tiếp
Cho tứ diện đều ABCD, M là trung điểm của BC. Khi đó cosin của góc giữa hai đường thẳng nào sau đây có giá trị bằng 3 6
A. (AB, DM).
B. (AD, DM).
C. (AM, DM).
D. (AB, AM).