Các câu hỏi tương tự
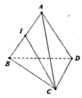
Cho tứ diện đều ABCD cạnh bằng a. Gọi M là trung điểm của CD. Tính khoảng cách giữa hai đường thẳng AC và BM
Đọc tiếp
Cho tứ diện đều ABCD cạnh bằng a. Gọi M là trung điểm của CD. Tính khoảng cách giữa hai đường thẳng AC và BM
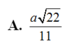
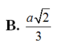
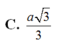
![]()
Cho tứ diện đều ABCD, M là trung điểm BC. Tính cosin của góc giữa hai đường thẳng AB và DM
A. 3 6
B. 2 2
C. 3 2
D. 1 2
Cho lăng trụ tam giác ABC.ABC có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của A’ trên mặt phẳng (ABC) là trung điểm O của cạnh AB. Số đo của góc giữa đường thẳng AA và mặt phẳng
(
A
B
C
)
bằng
60
0
. Gọi I là trung điểm của cạnh B’C’. Khoảng cách giữa hai đường thẳng CI và AB’ bằng
Đọc tiếp
Cho lăng trụ tam giác ABC.A'B'C' có đáy ABC là tam giác đều cạnh a. Hình chiếu vuông góc của A’ trên mặt phẳng (ABC) là trung điểm O của cạnh AB. Số đo của góc giữa đường thẳng AA' và mặt phẳng ( A ' B ' C ' ) bằng 60 0 . Gọi I là trung điểm của cạnh B’C’. Khoảng cách giữa hai đường thẳng CI và AB’ bằng
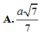
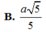
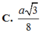
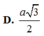
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng
60
0
. Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC.
Đọc tiếp
Cho hình chóp S.ABCD có đáy là hình vuông cạnh 2a, tam giác SAB đều, góc giữa (SCD) và (ABCD) bằng 60 0 . Gọi M là trung điểm của cạnh AB. Biết hình chiếu vuông góc của đỉnh S trên mặt phẳng (ABCD) nằm trong hình vuông ABCD. Tính theo a khoảng cách giữa hai đường thẳng SM và AC.
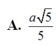
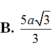
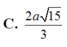
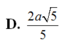
Cho hai đoạn thẳng AB và CD chéo nhau, AC là đường vuông góc chung của chúng. Biết rằng AC = h, AB = a, CD = b và góc giữa hai đường thẳng AB và CD bằng 600. Hãy tính thể tích của khối tứ diện ABCD.
Cho tứ diện ABCD có AB 2a, tam giác BCD vuông tại C, BD 2a, BC a và
2
A
C
2
-
A
D
2
6
a
2
Gọi E là trung điểm cạnh BD. Góc giữa hai đường thẳng AB và EC bằng A.
30
o
B.
90
°
C.
45
o...
Đọc tiếp
Cho tứ diện ABCD có AB = 2a, tam giác BCD vuông tại C, BD = 2a, BC = a và 2 A C 2 - A D 2 = 6 a 2 Gọi E là trung điểm cạnh BD. Góc giữa hai đường thẳng AB và EC bằng
A. 30 o
B. 90 °
C. 45 o
D. 60 o
Cho tứ diện đều ABCD, gọi M, N lần lượt là trung điểm của các cạnh AB, CD. Gọi
α
là số đo của góc giữa hai đường thẳng AN, CM. Khi đó
cos
α
bằng
Đọc tiếp
Cho tứ diện đều ABCD, gọi M, N lần lượt là trung điểm của các cạnh AB, CD. Gọi α là số đo của góc giữa hai đường thẳng AN, CM. Khi đó cos α bằng
![]()
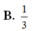
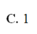
![]()
Cho tứ diện đều ABCD. Gọi M, N. P lần lượt là trung điểm của các cạnh AB, BC. AD và G là trọng tâm của tam giác BCD. Gọi
α
là số đo của góc giữa hai đường thẳng MG và NP. Khi đó
cos
α
bằng
Đọc tiếp
Cho tứ diện đều ABCD. Gọi M, N. P lần lượt là trung điểm của các cạnh AB, BC. AD và G là trọng tâm của tam giác BCD. Gọi α là số đo của góc giữa hai đường thẳng MG và NP. Khi đó cos α bằng
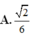
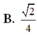
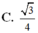
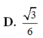
Cho tứ diện đều ABCD cạnh a, tính khoảng cách giữa hai đường thẳng AB và CD. A.
a
2
2
B.
a
3
2
C.
a
3...
Đọc tiếp
Cho tứ diện đều ABCD cạnh a, tính khoảng cách giữa hai đường thẳng AB và CD.
A. a 2 2
B. a 3 2
C. a 3 3
D. a