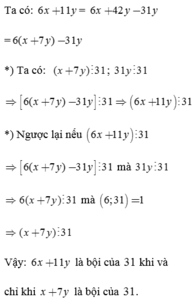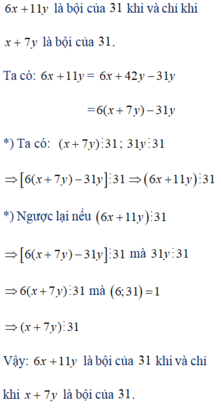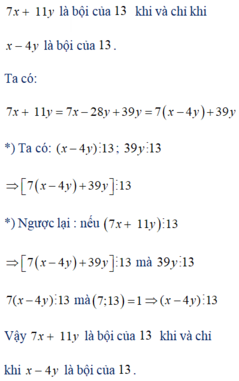Chứng minh : 5a + 47b là bội của 17 khi và chỉ khi a + 6b là bội của 17

Những câu hỏi liên quan
Câu a) Chứng tỏ 22a-b;8a+20b; 11a+10b chia hết cho 7 biết (a-b) chia hết cho 7
Câu b) chứng minh 5a+47b là bội của 17 khi và chỉ khi a+6b lag bội của 17
Cho x, y thuộc Z. Chứng minh rằng: 5x + 47y là bội của 17 khi và chỉ khi x + 6y là bội của 17.
5x + 47y (1)
= 5x + 30y + 17y = 5(x+6y) + 17y.
17y luôn chia hết cho 17. Vậy để (1) chia hết cho 17 <=> x + 6y chia hết 17
Đúng 0
Bình luận (0)
giải cho hẳn hoi thế này bố ai mà hiểu
Đúng 1
Bình luận (0)
Ta có :5x+47y = 5x+30y+17y
=5x+5.6.y+17y
=5(x+6y)+17y
Vì 17y chia hết cho 17 => 5.(x+6y) chia hết cho 17
Mà 5 ko chia hết cho 17 =>muốn 5.(x+6y) chia hết cho 17 thì x+6y phải chia hêt cho 17
Bài 1 : Cho x , y là các số nguyên . Chứng tỏ rằng 5x + 7y là bội của 17 khi và chỉ khi x + 6y là bội của 17 ( Trình bày rõ => like )
Ta có: x + 6y chia hết cho 17 => 5(x + 6y) chia hết cho 17
=> 5x + 30y chia hết cho 17
Lại có : 5x + 30y chia hét cho 17
17y chia hết cho 17
=> 5x + 30y + 17 chia hết cho 17
5x + 47y chia hết cho 17
Vậy 5x + 47y chia hết cho 17
Đúng thì tick nha! Hà My Trần
Đúng 0
Bình luận (0)
ta có 5x+7y chia hết cho 17 <=> x+6y chia hết cho 17
ta đặt M= 4(x+6y)-(5x+7y)
=>M=17y chia hết cho 17
Mà 5x+7y chia hết cho 17 ; M cũng chia hết cho 17
=> x+6y chia hết cho 17 vì (17;4)=1
vậy 5x+7y chia hết cho 17<=> x+6y chia hết cho 17
lưu ý: chia hết và bộ cũng giống nhau
Đúng 0
Bình luận (0)
cho x , y thuộc z CMR 5x + 47y là bội của 17 khi và chỉ khi x + 6 y là bội của 17
Với x+6y chia hết cho 17
Ta có
\(3\left(5x+47y\right)+2\left(x+6y\right)\)
\(=15x+141y+2x+12y\)
\(=17x+153y\) chia hết cho 17
Mặt khác 2(x+6y) chia hết cho 17
=> 3(5x+47y) chia hết cho 17
Mà (3;47)=1
=> 5x+47y chia hết cho 17
=> đpcm
Đúng 1
Bình luận (0)
Câu hỏi của Công Chúa Tình Yêu - Toán lớp 6 | Học trực tuyến
Đúng 0
Bình luận (2)
chờ x,y thuộc số nguyên.chứng minh rằng 5xX+47y là bội của 17 khi và chỉ khi x+6y là bội của 17
đây là toán nâng cao ai giải dùng mình tích luôn đồng thời mình sẽ kết bạn
5x + 47y = x + 6y + 4x + 24y + 17y = ( x + 6y ) + 4( x + 6y) + 17y = ( x + 6y ) ( 1 + 4 ) + 17y = 5 ( x + 6y ) + 17y
Vì 17y luôn chia hết cho 17 nên 5 ( x+ 6y ) + 17y \(⋮\)17 \(\Leftrightarrow\)x + 6y \(⋮\)17
Đúng 0
Bình luận (0)
Cho x, y thuộc Z. Chứng minh rằng 7x + 11y là bội của 13 khi và chỉ khi x – 4y là bội của 13.
Cho x, y thuộc Z. Chứng minh rằng 6x + 11y là bội của 31 khi và chỉ khi x + 7y là bội của 31.
Cho x, y thuộc Z. Chứng minh rằng
6x + 11y là bội của 31 khi và chỉ khi x + 7y là bội của 31
Cho x, y thuộc Z. Chứng minh rằng 7x + 11y là bội của 13 khi và chỉ khi x - 4y là bội của 13