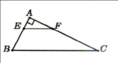
ΔABC vuông tại A, BC = 3√5cm. Hình vuông ADEF có cạnh 2cm, D ∈ AB, E ∈ BC, F ∈ AC. Tính AB, AC

Những câu hỏi liên quan
Cho tam giác ABC vuông tại A, BC= \(3\sqrt{5}\)cm. Hình vuông ADEF cạnh 2cm có D thuộc AB, E thuộc BC, F thuộc AC. Tính độ dài các cạnh AC, AB
Đặt \(\hept{\begin{cases}AB=x\\AC=y\end{cases}\left(x,y>0\right)}\)
Theo định lí Thales \(\frac{EF}{AB}=\frac{CF}{CA}\Rightarrow\frac{AB-EF}{AB}=\frac{CA-CF}{CA}\)
Hay \(\frac{x-2}{x}=\frac{2}{y}\Leftrightarrow xy=2\left(x+y\right)\left(1\right)\)
Theo định lí Pytagoras: \(AB^2+AC^2=BC^2\)hay \(x^2+y^2=45\left(2\right)\)
Từ (1),(2); ta có hệ phương trình: \(\hept{\begin{cases}xy=2\left(x+y\right)\\x^2+y^2=45\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x^2+y^2-45=0\\x^2+2xy+y^2-4\left(x+y\right)-45=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x^2+y^2-45=0\\\left(x+y\right)^2-4\left(x+y\right)-45=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x+y=9\\x^2+y^2-45=0\end{cases}}\)(Vì x,y dương)
\(\Leftrightarrow\hept{\begin{cases}y=9-x\\x^2+\left(9-x\right)^2-45=0\end{cases}}\Leftrightarrow\hept{\begin{cases}y=9-x\\x=6\left(h\right)x=3\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=6\\y=3\end{cases}}\left(h\right)\hept{\begin{cases}x=3\\y=6\end{cases}}\)
Vậy \(AB=3,AC=6\) hoặc \(AB=6,AC=3.\)
cho tam giác ABC vuông tại A, hình vuông ADEF với D thuộc AB, E thuộc BC, F thuộc AC.
a,c/m: BD.CF=\(\dfrac{AE^2}{2}\)
b,chứng minh: \(\dfrac{BD}{CF}=\dfrac{AB2}{AC^2}\)
c,hình vuông ADEF có cạnh = 2,BC=3\(\sqrt{5}\). Tính độ dài AB,Ac
Cho tam giác ABC vuông tại A, BC=\(3\sqrt{5}\)cm. Hình vuông ADEF cạnh 2 cm có D thuộc AB, E thuộc BC, F thuộc AC. Tính các độ dài AC, AB
Vì DE // AC Theo hệ quảTa lét ta có : \(\frac{DB}{AB}=\frac{DE}{AC}\Rightarrow\frac{AB-AD}{AB}=\frac{DE}{AC}\)
\(\Rightarrow\frac{AB-2}{AB}=\frac{2}{AC}\Rightarrow AB.AC-2AC=2AB\)
\(\Rightarrow AB.AC-2\left(AC+AB\right)=0\)(*)
Theo định lí Pytago tam giác ABC vuông tại A
\(BC^2=AB^2+AC^2\)(**)
Từ (*) ; (**) ta có hệ : \(\hept{\begin{cases}AB.AC-2\left(AC+AB\right)=0\\AB^2+AC^2=45\end{cases}}\)
bấm casio nhé, mode 9 _ 1 _ ấn hệ ra _ ''=''
MN ơi giải giúp mk bài này vs: Cho tam giác ABC vuông tại A , \(BC=3\sqrt{5}\). Một hình vuông ADEF có cạnh AD=2 VÀ D thuộc AB, E thuộc BC, F thuộc AC. Biết AB>AC, và diện tích ADEF=\(\frac{4}{9}\)diện tích ABC, tính AB, AC
Kẻ đường cao AH của tam giác ABC. Ta có: SADEF = 2.2=4 => SABC = 9. Ta có :\(S_{ABC}=\frac{1}{2}.BC.AH=\frac{1}{2}.3\sqrt{5}.AH=9\Rightarrow AH=\frac{6}{\sqrt{5}}\).
Áp dụng ĐL Py-ta-go ta tính được \(AE=\sqrt{2^2+2^2}=2\sqrt{2}>\frac{6}{\sqrt{5}}\Rightarrow E\ne H\Rightarrow\)Tam giác AEH vuông tại H.
Ta có: \(\sin AEH=\frac{AH}{AE}=\frac{3}{\sqrt{10}}\Rightarrow AEH\approx71^034'\)=>Góc ECA = 180o-góc EAC-góc AEC = 180o - 45o - 71o34' = 63o26'
\(\Rightarrow\sin BCA=\sin63^026'=\frac{AB}{BC}\approx0,894\Rightarrow AB\approx6\left(cm\right)\). Vận dụng ĐL Py-ta-go ta có:
\(AC=\sqrt{BC^2-AB^2}=3\)
Đúng 0
Bình luận (0)
ΔABC vuông tại A, BC = 3√5cm. Hình vuông ADEF có cạnh 2cm, D ∈ AB, E ∈ BC, F ∈ AC
a) Tính AB, AC
b) SABC, chu vi ΔABC
Cho tam giác ABC vuông tại A có AB = 6cm, BC = 10cm. Kẻ một đường thẳng song song với BC, cắt các cạnh AB và AC tại E và F. Biết AE = 2cm, tính tỉ số đồng dạng của Δ A E F , Δ A B C và độ dài các đoạn cạnh AF, EF
cho tam giác ABC vuông tại A gọi D,E,F lần lượt là trung điểm của các cạnh AB,BC,AC.Lấy điểm K là điểm đối xứng của điểm E qua AC
a)các tứ giác ADEF và AKCE là hình gì? vì sao?
b) cho AB=4cm và AC=5cm. Tính diện tích tam giác ABC
a: Xét ΔCAB có CF/CA=CE/CB
nên FE//AB và FE=AB/2
=>FE//AD và FE=AD
Xét tứ giác AFED có
FE//AD
FE=AD
góc FAD=90 độ
Do đó: AFED là hình chữ nhật
Xét tứ giác AECK có
F là trung điểm chung của AC và EK
EA=EC
Do đó: AECK là hình thoi
b: \(S_{ABC}=\dfrac{1}{2}\cdot4\cdot5=10\left(cm^2\right)\)
Đúng 0
Bình luận (0)
cho tam giác ABC vuông tại A gọi D,E,F lần lượt là trung điểm của các cạnh AB,BC,AC.Lấy điểm K là điểm đối xứng của điểm E qua ACa)các tứ giác ADEF và AKCE là hình gì? vì sao?b) cho AB4cm và AC5cm. Tính diện tích tam giác ABC
Đọc tiếp
cho tam giác ABC vuông tại A gọi D,E,F lần lượt là trung điểm của các cạnh AB,BC,AC.Lấy điểm K là điểm đối xứng của điểm E qua AC
a)các tứ giác ADEF và AKCE là hình gì? vì sao?
b) cho AB=4cm và AC=5cm. Tính diện tích tam giác ABC
a: Xét ΔCAB có CF/CA=CE/CB
nên FE//AB và FE=AB/2
=>FE//AD và FE=AD
Xét tứ giác AFED có
FE//AD
FE=AD
góc FAD=90 độ
Do đó: AFED là hình chữ nhật
Xét tứ giác AECK có
F là trung điểm chung của AC và EK
EA=EC
Do đó: AECK là hình thoi
b: \(S_{ABC}=\dfrac{1}{2}\cdot4\cdot5=10\left(cm^2\right)\)
Đúng 0
Bình luận (0)
✿Cho tam giác ABC vuông tại a có AB< AC. Gọi D và E lần lượt là trung điểm của các cạnh AC và BC, kẻ EF vuông góc AB tại F a. Chứng minh ADEF là hình chữ nhật b. Gọi G là điểm đối xứng qua D. Chứng minh AECG là hình thoi c. Kẻ EH vuông góc AG. Chứng minh DH vuông góc với HF
Xem chi tiết