Cho(O) và (I) lần lượt là đường tròn ngoại tiếp và nội tiếp một tam giác đều. Nếu S1 và S2 lần lượt là diện tích hình tròn (O) và (I) thì tỉ số S1/S2 bằng

Những câu hỏi liên quan
Một hình lập phương cạnh bằng a nội tiếp khối cầu
S
1
và ngoại tiếp khối cầu
S
2
, gọi
V
1
và
V
2
lần lượt là thể tích của các khối
S
1
và
S
2
. Tính tỉ số
k...
Đọc tiếp
Một hình lập phương cạnh bằng a nội tiếp khối cầu S 1 và ngoại tiếp khối cầu S 2 , gọi V 1 và V 2 lần lượt là thể tích của các khối S 1 và S 2 . Tính tỉ số k = V 1 V 2 .
A. k = 1 2 2
B. k = 1 3 3
C. k = 2 2
D. 3 3
Đáp án D
Gọi khối lập phương cần xét ABCD.A'B'C'D' cạnh a.
Bán kính mặt cầu ngoại tiếp khối cầu là R 2 = A A ' 2 = a 2 ⇒ V 1 = 4 3 R 2 3 .
Bán kính mặt cầu ngoại tiếp khối cầu là
R 1 = A C ' 2 = A B 2 + A D 2 + A A ' 2 2 = a 3 2 ⇒ V 1 = 4 3 πR 3 1
Vậy tỉ số k = V 1 V 2 = R 3 1 R 3 1 = R 1 R 2 3 = 3 3 = 3 3 .
Đúng 0
Bình luận (0)
Cho tứ diện đều ABCD có mặt cầu nội tiếp là
S
1
và mặt cầu ngoại tiếp là
S
2
. Một hình lập phương ngoại tiếp
S
2
và nội tiếp trong mặt cầu
S
2
. Gọi
r
1
,
r
2
,
...
Đọc tiếp
Cho tứ diện đều ABCD có mặt cầu nội tiếp là S 1 và mặt cầu ngoại tiếp là S 2 . Một hình lập phương ngoại tiếp S 2 và nội tiếp trong mặt cầu S 2 . Gọi r 1 , r 2 , r 3 lần lượt là bán kính các mặt cầu S 1 , S 2 , S 3 . Khẳng định nào sau đây đúng?
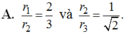
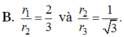
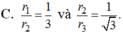
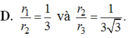
Cho tứ diện đều ABCD có mặt cầu nội tiếp là
S
1
và mặt cầu ngoại tiếp là
S
2
. Một hình lập phương ngoại tiếp
S
2
và nội tiếp trong mặt cầu
S
2
. Gọi
r
1
,
r
2...
Đọc tiếp
Cho tứ diện đều ABCD có mặt cầu nội tiếp là S 1 và mặt cầu ngoại tiếp là S 2 . Một hình lập phương ngoại tiếp S 2 và nội tiếp trong mặt cầu S 2 . Gọi r 1 , r 2 , r 3 lần lượt là bán kính các mặt cầu ( S 1 ) , ( S 2 ) , ( S 3 ) . Khẳng định nào sau đây đúng?
A. r 1 r 2 = 2 3 và r 2 r 3 = 1 2 .
B. r 1 r 2 = 2 3 và r 2 r 3 = 1 3 .
C. r 1 r 2 = 1 3 và r 2 r 3 = 1 3 .
D. r 1 r 2 = 1 3 và r 2 r 3 = 1 3 3 .
Cho tứ diện đều ABCD có mặt cẩu nội tiếp là (S1) và mặt cầu ngoại tiếp là (S2). Một hình lập phương ngoại tiếp (S2) và nội tiếp trong mặt cầu (S3). Gọi
r
1
,
r
2
,
r
3
lần lượt là bán kính các mặt cầu (S1), (S2), (S3). Khẳng định nào sau đây là đúng A.
r
1
r
2...
Đọc tiếp
Cho tứ diện đều ABCD có mặt cẩu nội tiếp là (S1) và mặt cầu ngoại tiếp là (S2). Một hình lập phương ngoại tiếp (S2) và nội tiếp trong mặt cầu (S3). Gọi r 1 , r 2 , r 3 lần lượt là bán kính các mặt cầu (S1), (S2), (S3). Khẳng định nào sau đây là đúng
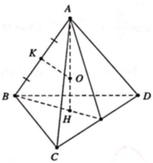
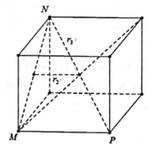
A. r 1 r 2 = 2 3 và r 2 r 3 = 1 3
B. r 1 r 2 = 2 3 và r 2 r 3 = 1 2
C. r 1 r 2 = 1 3 và r 2 r 3 = 1 3
D. r 1 r 2 = 1 3 và r 2 r 3 = 1 3 3
Cho một hình trụ có hai đáy là hai đường tròn (O;R), với OO
R
3
và một hình nón có đỉnh O’ và đáy là hình tròn (O;R), Ký hiệu
S
1
,
S
2
lần lượt là diện tích xung quanh của hình trụ và hình nón. Tính k
S
1
/
S
2
A. k 1/3 B. k C C. k
3
D. k 1/2
Đọc tiếp
Cho một hình trụ có hai đáy là hai đường tròn (O;R), với OO'= R 3 và một hình nón có đỉnh O’ và đáy là hình tròn (O;R), Ký hiệu S 1 , S 2 lần lượt là diện tích xung quanh của hình trụ và hình nón. Tính k= S 1 / S 2
A. k= 1/3
B. k= C
C. k= 3
D. k= 1/2
Cho hình lập phương có cạnh bằng 40cm và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi
S
1
,
S
2
lần lượt là diện tích toàn phần của hình lập phương và diện tích toàn phần của hình trụ. Tính
S
S
1
+
S
2
(
c
m...
Đọc tiếp
Cho hình lập phương có cạnh bằng 40cm và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S 1 , S 2 lần lượt là diện tích toàn phần của hình lập phương và diện tích toàn phần của hình trụ. Tính S = S 1 + S 2 ( c m 2 )
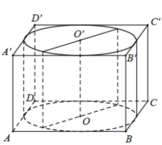
![]()
![]()
![]()
![]()
Cho hình lập phương có cạnh bằng 40cm và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi
S
1
,
S
2
lần lượt là diện tích toàn phần của hình lập phương và diện tích toàn phần của hình trụ. Tính
S
S
1
+
S
2
c
m...
Đọc tiếp
Cho hình lập phương có cạnh bằng 40cm và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S 1 , S 2 lần lượt là diện tích toàn phần của hình lập phương và diện tích toàn phần của hình trụ. Tính S = S 1 + S 2 c m 2
A. S = 4 2400 + π
B. S = 2400 4 + 2 π
C. S = 2400 4 + 3 π
D. S = 4 2400 + 3 π
Đáp án B
Bán kính đáy của hình trụ là R = 20 cm
Diện tích toàn phần của hình lập phương là S 1 = 6 . 40 2 = 9600 c m 2
Diện tích toàn phần của hình trụ là S 2 = 2 πRh + 2 πR 2 = 2 π 20 . 40 + 2 π 40 2 = 4800 cm 2
Vậy tổng S = S 1 + S 2 = 9600 + 4800 π = 2400 4 + 2 π cm 2
Đúng 0
Bình luận (0)
Cho hình lập phương có cạnh 40cm và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi
S
1
,
S
2
lần lượt là diện tích toàn phần của hình lập phương và diện tích toàn phần của hình trụ. Tính
S
S
1
+
S
2
(
c
m
2
)...
Đọc tiếp
Cho hình lập phương có cạnh 40cm và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S 1 , S 2 lần lượt là diện tích toàn phần của hình lập phương và diện tích toàn phần của hình trụ. Tính S = S 1 + S 2 ( c m 2 )
A. S=4(2400+ π )
B. S=2400(4+ π )
C. S=2400(4+3 π )
D. S=4(2400+3 π )
Cho hình lập phương có cạnh 40 cm và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi
S
1
;
S
2
lần lượt là diện tích toàn phần của hình lập phương và diện tích toàn phần của hình trụ. Tính
S
S
1
+
S
2...
Đọc tiếp
Cho hình lập phương có cạnh 40 cm và một hình trụ có hai đáy là hai hình tròn nội tiếp hai mặt đối diện của hình lập phương. Gọi S 1 ; S 2 lần lượt là diện tích toàn phần của hình lập phương và diện tích toàn phần của hình trụ. Tính S = S 1 + S 2 ?
A. S = 4 ( 2400 + π )
B. S = 2400 ( 4 + π )
C. S = 2400 ( 4 + 3 π )
D. S = 4 ( 2400 + 3 π )